Question

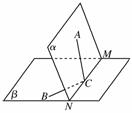
如图，已知平面α∩平面β＝MN，A∈α，B∈β，C∈MN，且∠ACM＝60°，∠BCN＝45°，二面角A－MN－B＝60°，AC＝2.

(1)求点A到平面β的距离；

(2)设二面角A－BC－M的大小为θ，求tan θ的值．

Answer 1

 解：(1)如图，作AO⊥β于O，

AD⊥MN于D，连接OD，

知∠ADO＝60°.在Rt△ADC中，

易得AD＝，CD＝1.

在Rt△ADO中，OD＝，

AO＝×sin 60°＝.

(2)

如图，在β平面内，过点O作直线BC的垂线，垂足为F，与直线MN交于E点，易证∠AFO为二面角A－BC－M的平面角，由已知得∠BCN＝∠ECF＝∠CEF＝∠DEF＝45°，

可求得OE＝，DE＝DO＝，EC＝1－，

EF＝×(1－)＝，

OF＝OE＋EF＝＋＝，

tan θ＝＝＝6－3.