题目内容
已知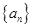 为等差数列,
为等差数列,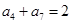 ,
,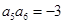 ,则
,则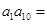 ( )
( )
A.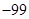 | B.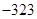 | C.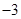 | D.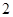 |
B
解析试题分析:根据题意可知,由于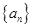 为等差数列,
为等差数列,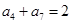 ,
,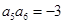 ,那么可知
,那么可知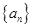 为等差数列,
为等差数列, ,则可以将
,则可以将 看作一元二次方程的两个根,结合已知的条件可知
看作一元二次方程的两个根,结合已知的条件可知
考点:等差数列 ,因此可知
,因此可知
当d=-4或者d=4时,可知对应的结论为-323,故选B.
点评:考查了等差数列的通项公式的运用,属于常规试题,解决出基本量即可。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知等差数列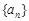 公差
公差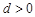 ,前n项和为
,前n项和为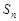 .则“
.则“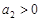 ”是“数列
”是“数列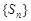 为递增数列”的
为递增数列”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充也不必要条件 |
数列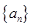 的首项为
的首项为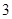 ,
,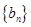 为等差数列且
为等差数列且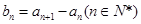 .若则
.若则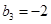 ,
,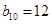 ,则
,则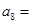 ( )
( )
| A.0 | B.3 | C.8 | D.11 |
在等差数列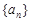 中,已知
中,已知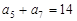 ,则该数列前11项和
,则该数列前11项和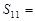
| A.196 | B.132 | C.88 | D.77 |
首项为 的等差数列,从第10项起开始为正数,则公差d的取值范围是
的等差数列,从第10项起开始为正数,则公差d的取值范围是
A.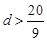 | B.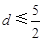 | C.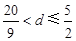 | D.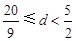 |
数列 是等差数列,
是等差数列,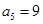 ,
, ,则
,则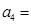
A.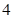 | B.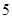 | C.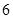 | D.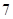 |
观察下列各式: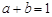 ,
,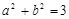 ,
,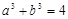 ,
, 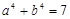 ,
,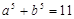 ,…,则
,…,则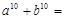
| A.199 | B.123 | C.76 | D.28 |
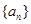 中,
中,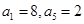 ,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是( )
,若在每相邻两项间各插入一个数,使之成等差数列,那么新的等差数列的公差是( )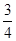
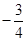
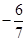
 的前10项中,所有偶数项、所有奇数项之和分别为55和45,则它的首项
的前10项中,所有偶数项、所有奇数项之和分别为55和45,则它的首项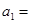 _______。
_______。