题目内容
已知函数f(x)=2sinx(sinx+cosx).(1)求f(x)的最小正周期;
(2)当
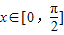 时,求f(x)的最大值.
时,求f(x)的最大值.
【答案】分析:根据同角三角函数的基本关系进行化简求解即可.
解答:解:
f(x)=2sinx(sinx+cosx)=2sin2x+2sinxcosx…(1分)
=1-cos2x+sin2x…(2分)
=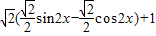 …(3分)
…(3分)
=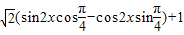 …(4分)
…(4分)
=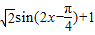 …(5分)
…(5分)
(1)f(x)的最小正周期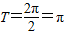 …(7分)
…(7分)
(2)∵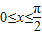 ,∴
,∴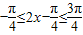 …(8分)
…(8分)
∴当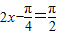 ,即
,即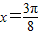 时,f(x)取得最大值…(10分)
时,f(x)取得最大值…(10分)
且最大值为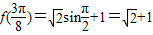 …(12分)
…(12分)
点评:本题主要考查同角三角函数的基本关系、二倍角公式的应用,属于基础题.
解答:解:
f(x)=2sinx(sinx+cosx)=2sin2x+2sinxcosx…(1分)
=1-cos2x+sin2x…(2分)
=
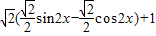 …(3分)
…(3分)=
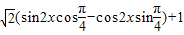 …(4分)
…(4分)=
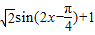 …(5分)
…(5分)(1)f(x)的最小正周期
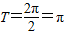 …(7分)
…(7分)(2)∵
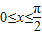 ,∴
,∴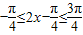 …(8分)
…(8分)∴当
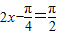 ,即
,即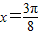 时,f(x)取得最大值…(10分)
时,f(x)取得最大值…(10分)且最大值为
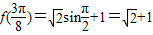 …(12分)
…(12分)点评:本题主要考查同角三角函数的基本关系、二倍角公式的应用,属于基础题.

练习册系列答案
相关题目