题目内容
【题目】已知椭圆![]() 为参数),
为参数), ![]() 是
是![]() 上的动点,且满足
上的动点,且满足![]() 为坐标原点),以原点
为坐标原点),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系,点
轴的正半轴为极轴建立坐标系,点![]() 的极坐标为
的极坐标为![]() .
.
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的普通方程;
的普通方程;
(2)利用椭圆![]() 的极坐标方程证明
的极坐标方程证明![]() 为定值,并求面积的最大值.
为定值,并求面积的最大值.
【答案】(1)![]() (2)最大值
(2)最大值![]() .
.
【解析】试题分析:(1)将![]() 的极坐标转化为平面直角坐标,由椭圆
的极坐标转化为平面直角坐标,由椭圆![]() 的参数方程,可设
的参数方程,可设![]() 点的坐标,利用中点坐标得出
点的坐标,利用中点坐标得出![]() 点坐标,消去参数可得轨迹
点坐标,消去参数可得轨迹![]() 的普通方程;(2)将椭圆的普通方程化为极坐标方程,可设
的普通方程;(2)将椭圆的普通方程化为极坐标方程,可设![]() 两点的极坐标,由题中所给
两点的极坐标,由题中所给![]() ,可得结论.
,可得结论.
试题解析:(1)点![]() 的直角坐标为
的直角坐标为![]() ,由题意可设点
,由题意可设点![]() 的坐标为
的坐标为![]() 参数,
参数,
则线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的参数方程为
的参数方程为 为参数)
为参数)
消去![]() 可得
可得![]() 的普通方程为
的普通方程为![]() .
.
(2)椭圆![]() 的普通方程为
的普通方程为![]() ,化为极坐标方程得
,化为极坐标方程得![]() ,
,
变形得![]() ,
,
由![]() ,不妨设
,不妨设![]() ,所以
,所以![]()
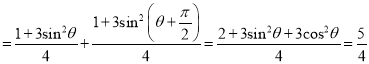 (定值),
(定值),
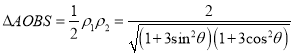
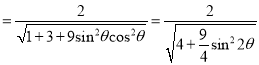
易知当![]() 时,
时, ![]() 取得最大值
取得最大值![]() .
.

【题目】目前我国城市的空气污染越来越严重,空气质量指数![]() 一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到
一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到![]() 列联表如下:
列联表如下:
室外工作 | 室内工作 | 合计 | |
有呼吸系统疾病 | 150 | ||
无呼吸系统疾病 | 100 | ||
合计 | 200 |
(Ⅰ)请把![]() 列联表补充完整;
列联表补充完整;
(Ⅱ)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(Ⅲ)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机抽取2人,求2人都有呼吸系统疾病的概率.
参考公式与临界表:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】微信红包是一款可以实现收发红包、查收记录和提现的手机应用.某网络运营商对甲、乙两个品牌各5种型号的手机在相同环境下抢到的红包个数进行统计,得到如下数据:
手机品牌 型号 | I | II | III | IV | V |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(乙) | 5 | 7 | 9 | 4 | 3 |
手机品牌 红包个数 | 优 | 非优 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(1)如果抢到红包个数超过5个的手机型号为“优”,否则为“非优”,请完成上述2×2列联表,据此判断是否有85%的把握认为抢到的红包个数与手机品牌有关?
(2)如果不考虑其他因素,要从甲品牌的5种型号中选出3种型号的手机进行大规模宣传销售.
①求在型号I被选中的条件下,型号II也被选中的概率;
②以![]() 表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量
表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 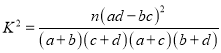 ,其中
,其中![]() .
.