题目内容
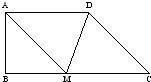 如图,在梯形ABCD中,∠C=45°,∠BAD=∠B=90°,AD=3,CD=2
如图,在梯形ABCD中,∠C=45°,∠BAD=∠B=90°,AD=3,CD=2| 2 |
分析:过D作DE⊥B以C于E,延长AB到P,使BP=AB=2,连接PD交BC于M′,根据两点之间线段最短可知此时△AM′D周长的最小.
解答:解:过D作DE⊥B以C于E,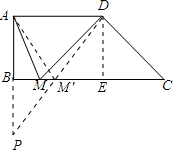
在Rt△CDE中,∠C=45°,CD=2
,
∴DE=2,
∴AB=2,
延长AB到P,使BP=AB=2,
连接PD交BC于M′,PD=
=5,
则△AMD的周长最小值:AD+DM′+AM′=AD+PD=8.
故选A.

在Rt△CDE中,∠C=45°,CD=2
| 2 |
∴DE=2,
∴AB=2,
延长AB到P,使BP=AB=2,
连接PD交BC于M′,PD=
| AD2+AP2 |
则△AMD的周长最小值:AD+DM′+AM′=AD+PD=8.
故选A.
点评:本题考查三角形周长最小值,考查学生分析解决问题的能力.凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
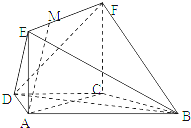 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.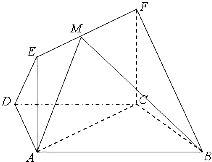 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.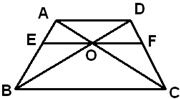 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.