题目内容
本题共有2个小题,第1小题满分8分,第2小题满分6分过直角坐标平面xOy中的抛物线y2?2px (p>0)的焦点F作一条倾斜角为
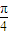 的直线与抛物线相交于A、B两点.
的直线与抛物线相交于A、B两点.(1)用p表示A、B之间的距离并写出以AB为直径的圆C方程;
(2)若圆C于y轴交于M、N两点,写出M、N的坐标,证明∠MFN的大小是与p无关的定值,并求出这个值.
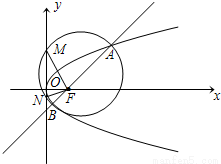
【答案】分析:(1)根据所给的抛物线的方程写出抛物线的焦点坐标,又有所给的直线的倾斜角得到这条直线的斜率,由点斜式写出直线的方程,要求两点之间的距离,首先要把直线与抛物线方程联立,整理出关于x的方程,根据根和系数之间的关系,和抛物线的定义,写出结果.
(2)由(1)得:圆C方程:(x-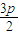 )2+(y-p)2=4p2,令x=0得到圆与y轴的交点坐标,利用到角公式求出∠MFN的正切值tan∠MFN,它是一与p无关的定值,并求出这个值即可.
)2+(y-p)2=4p2,令x=0得到圆与y轴的交点坐标,利用到角公式求出∠MFN的正切值tan∠MFN,它是一与p无关的定值,并求出这个值即可.
解答:解:(1)焦点F(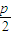 ,0),过抛物线的焦点且倾斜角为
,0),过抛物线的焦点且倾斜角为 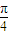 的直线方程是
的直线方程是 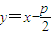
由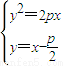
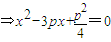
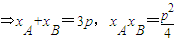 ⇒|AB|=xA+xB+p=4p,
⇒|AB|=xA+xB+p=4p,
AB的中点坐标为C(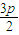 ,p),以AB为直径的圆C的半径为:2p,
,p),以AB为直径的圆C的半径为:2p,
∴以AB为直径的圆C方程:(x-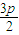 )2+(y-p)2=4p2,
)2+(y-p)2=4p2,
(2)由(1)得:圆C方程:(x-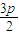 )2+(y-p)2=4p2,
)2+(y-p)2=4p2,
令x=0得:(0-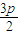 )2+(y-p)2=4p2,⇒yM=
)2+(y-p)2=4p2,⇒yM=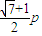 ,yN=
,yN=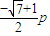 ,
,
∴tan∠MFN=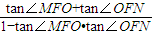 =
=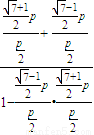 =-
=-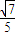 (定值).
(定值).
∴∠MFN=π-arctan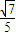 .
.
点评:本题考查直线与圆锥曲线之间的关系,实际上这种问题在解题时考虑的解题方法类似,都需要通过方程联立来解决问题,注意本题中抛物线还有本身的特点,注意使用,属中档题.
(2)由(1)得:圆C方程:(x-
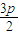 )2+(y-p)2=4p2,令x=0得到圆与y轴的交点坐标,利用到角公式求出∠MFN的正切值tan∠MFN,它是一与p无关的定值,并求出这个值即可.
)2+(y-p)2=4p2,令x=0得到圆与y轴的交点坐标,利用到角公式求出∠MFN的正切值tan∠MFN,它是一与p无关的定值,并求出这个值即可.解答:解:(1)焦点F(
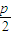 ,0),过抛物线的焦点且倾斜角为
,0),过抛物线的焦点且倾斜角为 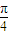 的直线方程是
的直线方程是 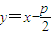
由
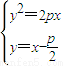
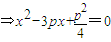
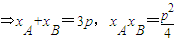 ⇒|AB|=xA+xB+p=4p,
⇒|AB|=xA+xB+p=4p,AB的中点坐标为C(
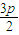 ,p),以AB为直径的圆C的半径为:2p,
,p),以AB为直径的圆C的半径为:2p,∴以AB为直径的圆C方程:(x-
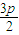 )2+(y-p)2=4p2,
)2+(y-p)2=4p2,(2)由(1)得:圆C方程:(x-
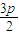 )2+(y-p)2=4p2,
)2+(y-p)2=4p2,令x=0得:(0-
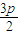 )2+(y-p)2=4p2,⇒yM=
)2+(y-p)2=4p2,⇒yM=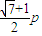 ,yN=
,yN=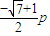 ,
,∴tan∠MFN=
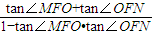 =
=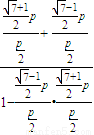 =-
=-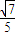 (定值).
(定值).∴∠MFN=π-arctan
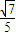 .
.点评:本题考查直线与圆锥曲线之间的关系,实际上这种问题在解题时考虑的解题方法类似,都需要通过方程联立来解决问题,注意本题中抛物线还有本身的特点,注意使用,属中档题.

练习册系列答案
相关题目
 (2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分
(2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分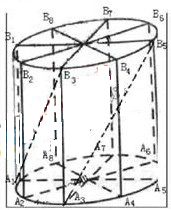 (1)当圆柱底面半径
(1)当圆柱底面半径 且与向量
且与向量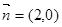 夹角为
夹角为 ,其中A,B,C是
,其中A,B,C是 的内角。
的内角。 的取值范围。
的取值范围。