题目内容
如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.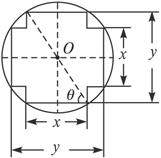
(1)将十字形的面积表示为θ的函数;
(2)θ为何值时,十字形的面积最大?最大面积是多少?
(1)解:设S为十字形的面积,则
S=2xy-x2=2sinθcosθ-cos2θ(![]() <θ<
<θ<![]() ).
).
(2)解法一:S=2sinθcosθ-cos2θ
=sin2θ-![]() cos2θ-
cos2θ-![]()
=![]() sin(2θ-φ)-
sin(2θ-φ)-![]() ,
,
其中φ=arccos![]() ,
,
当sin(2θ-φ)=1,即2θ-φ=![]() 时,S最大.
时,S最大.
所以,当θ=![]() +
+![]() arccos
arccos![]() 时,S最大,
时,S最大,
S的最大值为![]() .
.
解法二:因为S=2sinθcosθ-cos2θ,
所以S′=2cos2θ-2sin2θ+2sinθcosθ=2cos2θ+sin2θ.
令S′=0,即2cos2θ+sin2θ=0,
可解得θ=![]() +
+![]() arctan(-2).
arctan(-2).
所以,当θ=![]() +
+![]() arctan(-2)时,S最大,S的最大值为
arctan(-2)时,S最大,S的最大值为![]() .
.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.
如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.


