题目内容
已知m、n、s、t为正数,m+n=2,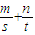 =9其中m、n是常数,且s+t最小值是
=9其中m、n是常数,且s+t最小值是 ,满足条件的点(m,n)是椭圆
,满足条件的点(m,n)是椭圆
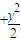 =1一弦的中点,则此弦所在的直线方程为( )
=1一弦的中点,则此弦所在的直线方程为( )A.x-2y+1=0
B.2x-y-1=0
C.2x+y-3=0
D.x+2y-3=0
【答案】分析:由题设知(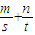 )(s+t)=n+m+
)(s+t)=n+m+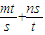 ≥
≥ =
=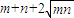 ,满足
,满足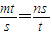 时取最小值,由此得到m=n=1.设以(1,1)为中点的弦交椭圆
时取最小值,由此得到m=n=1.设以(1,1)为中点的弦交椭圆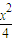
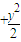 =1于A(x1,y1),B(x2,y2),由中点从坐标公式知x1+x2=2,y1+y2=2,把A(x1,y1),B(x2,y2)分别代入x2+2y2=4,得
=1于A(x1,y1),B(x2,y2),由中点从坐标公式知x1+x2=2,y1+y2=2,把A(x1,y1),B(x2,y2)分别代入x2+2y2=4,得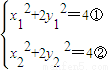 ,①-②,得2(x1-x2)+4(y1-y2)=0,k=
,①-②,得2(x1-x2)+4(y1-y2)=0,k=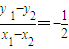 ,由此能求出此弦所在的直线方程.
,由此能求出此弦所在的直线方程.
解答:解:∵sm、n、s、t为正数,m+n=2,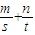 =9,
=9,
s+t最小值是 ,
,
∴(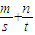 )(s+t)的最小值为4
)(s+t)的最小值为4
∴(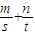 )(s+t)=n+m+
)(s+t)=n+m+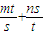 ≥
≥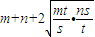 =
=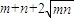 ,
,
满足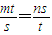 时取最小值,
时取最小值,
此时最小值为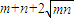 =2+2
=2+2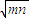 =4,
=4,
得:mn=1,又:m+n=2,所以,m=n=1.
设以(1,1)为中点的弦交椭圆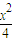
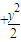 =1于A(x1,y1),B(x2,y2),
=1于A(x1,y1),B(x2,y2),
由中点从坐标公式知x1+x2=2,y1+y2=2,
把A(x1,y1),B(x2,y2)分别代入x2+2y2=4,得
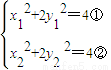 ,
,
①-②,得2(x1-x2)+4(y1-y2)=0,
∴k=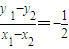 ,
,
∴此弦所在的直线方程为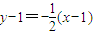 ,
,
即x+2y-3=0.
故选D.
点评:本题考查椭圆的性质和应用,解题时要认真审题,注意均值不等式和点差法的合理运用.
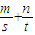 )(s+t)=n+m+
)(s+t)=n+m+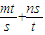 ≥
≥ =
=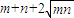 ,满足
,满足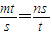 时取最小值,由此得到m=n=1.设以(1,1)为中点的弦交椭圆
时取最小值,由此得到m=n=1.设以(1,1)为中点的弦交椭圆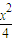
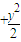 =1于A(x1,y1),B(x2,y2),由中点从坐标公式知x1+x2=2,y1+y2=2,把A(x1,y1),B(x2,y2)分别代入x2+2y2=4,得
=1于A(x1,y1),B(x2,y2),由中点从坐标公式知x1+x2=2,y1+y2=2,把A(x1,y1),B(x2,y2)分别代入x2+2y2=4,得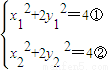 ,①-②,得2(x1-x2)+4(y1-y2)=0,k=
,①-②,得2(x1-x2)+4(y1-y2)=0,k=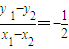 ,由此能求出此弦所在的直线方程.
,由此能求出此弦所在的直线方程.解答:解:∵sm、n、s、t为正数,m+n=2,
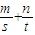 =9,
=9,s+t最小值是
 ,
,∴(
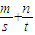 )(s+t)的最小值为4
)(s+t)的最小值为4∴(
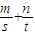 )(s+t)=n+m+
)(s+t)=n+m+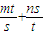 ≥
≥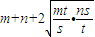 =
=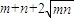 ,
,满足
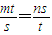 时取最小值,
时取最小值,此时最小值为
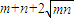 =2+2
=2+2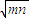 =4,
=4,得:mn=1,又:m+n=2,所以,m=n=1.
设以(1,1)为中点的弦交椭圆
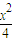
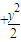 =1于A(x1,y1),B(x2,y2),
=1于A(x1,y1),B(x2,y2),由中点从坐标公式知x1+x2=2,y1+y2=2,
把A(x1,y1),B(x2,y2)分别代入x2+2y2=4,得
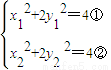 ,
,①-②,得2(x1-x2)+4(y1-y2)=0,
∴k=
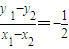 ,
,∴此弦所在的直线方程为
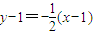 ,
,即x+2y-3=0.
故选D.
点评:本题考查椭圆的性质和应用,解题时要认真审题,注意均值不等式和点差法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目