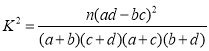题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 在其定义域内单调递增,求实数
在其定义域内单调递增,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的图象与
的图象与![]() 轴相切?若存在,求满足条件的
轴相切?若存在,求满足条件的![]() 的取值范围,请说明理由.
的取值范围,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据导数和函数的单调性的关系,分离参数,即可求出![]() 的取值范围;
的取值范围;
(2)函数![]() 的图象与
的图象与![]() 轴相切,且存在
轴相切,且存在![]() 的极值等于0,根据导数和函数的极值的关系即可求出答案.
的极值等于0,根据导数和函数的极值的关系即可求出答案.
(1)![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,在
,在![]() 上恒成立,
上恒成立,
即![]() ,
,
易知![]() 在
在![]() 上为增函数,
上为增函数,
∴![]() ,
,
∴![]() ;
;
(2)函数![]() ,
,
设![]() ,
,
∴![]()
![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
①当![]() 时,即
时,即![]() 时,当
时,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() ,解得
,解得![]() (舍去),
(舍去),
②当![]() 时,
时,![]() ,即极值点为
,即极值点为![]() 或
或![]() ,
,
∵函数![]() 的图象与
的图象与![]() 轴相切,
轴相切,
∴![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
当![]() 时,可得
时,可得![]() ,
,
设![]() ,则
,则![]() ,
,
则![]() ,
,
即![]() ,
,
设![]() ,
,
∴![]() ,
,
再令![]()
∴![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
∴![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∵![]() ,
,
∴存在![]() ,使得
,使得![]() ,
,
即![]() ,即
,即![]() ,
,
综上所述存在实数一个实数![]() ,得使得函数
,得使得函数![]() 的图象与
的图象与![]() 轴相切.
轴相切.

 课时训练江苏人民出版社系列答案
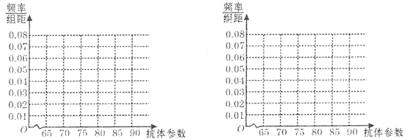
课时训练江苏人民出版社系列答案【题目】科学家为研究对某病毒有效的疫苗,通过小鼠进行毒性和药效预实验.为了比较注射A,B两种疫苗后产生的抗体情况,选200只小鼠做实验,将这200只小鼠随机分成两组,每组100只,其中一组注射疫苗A,另一组注射疫苗B.下表1和表2分别是注射疫苗A和疫苗B后的实验结果.
表1:注射疫苗A后产生抗体参数的频率分布表
抗体参数 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2:注射疫苗B后产生抗体参数的频率分布表
抗体参数 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
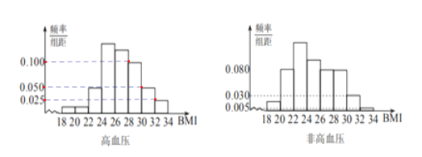
(1)完成下面频率分布直方图,并比较注射两种疫苗后抗体参数的中位数大小;
(2)完成下面2×2列联表,并回答能否有99.9%的把握认为“注射疫苗A后的抗体参数与注射疫苗B后的抗体参数有差异”.
表3:
抗体参数小于75 | 抗体参数不小于75 | 合计 | |
注射疫苗A | a= | b= | |
注射疫苗B | c= | d= | |
合计 | n= |
附: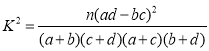
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 10.828 |