题目内容
17.由$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,$\sqrt{4+\frac{4}{15}}=4\sqrt{\frac{4}{15}}$,$\sqrt{5+\frac{5}{24}}=5\sqrt{\frac{5}{24}}$,…,$\sqrt{10+\frac{a}{b}}=10\sqrt{\frac{a}{b}}$,推测a+b=109.分析 本题考查的知识点是归纳推理,方法是根据已知中的等式,分析根号中分式分子和分母的变化规律,得到a,b值.
解答 解:由已知中,
$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,
$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,
$\sqrt{4+\frac{4}{15}}=4\sqrt{\frac{4}{15}}$,
$\sqrt{5+\frac{5}{24}}=5\sqrt{\frac{5}{24}}$,
…,
归纳可得:第n个等式为:$\sqrt{(n+1)+\frac{n+1}{(n+1)^{2}-1}}=(n+1)\sqrt{\frac{n+1}{(n+1)^{2}-1}}$,
当n+1=10时,a=10,b=99,
故a+b=109,
故答案为:109
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
7.如果执行下面的框图,若输入的m,n的值分别为392,252,则输出的结果m=( )
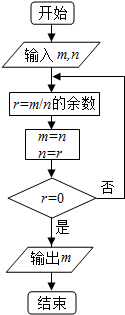

| A. | 7 | B. | 14 | C. | 21 | D. | 28 |
8.程序框图中表示计算、赋值功能的是( )
| A. |  | B. |  | C. |  | D. |  |
12.若执行如图的程序框图,则输出的s值是( )


| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
2.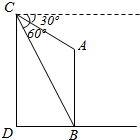 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )| A. | 30m | B. | 20$\sqrt{3}$m | C. | $\frac{40\sqrt{3}}{3}$m | D. | 40m |
9.分式$\frac{6{x}^{2}+12x+10}{{x}^{2}+2x+2}$可取的最小值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 不存在 |
6.在△ABC中,a,b,c分别为内角A,B,C的对边,若2b=a+c,且B=$\frac{π}{4}$,则cosA-cosC的值为( )
| A. | $\sqrt{2}$ | B. | $±\sqrt{2}$ | C. | $\root{4}{2}$ | D. | ±$\root{4}{2}$ |
7.已知x,y是三角形的两边,α,β是三角形的两内角,且x,y,α,β之间满足下列关系$\left\{\begin{array}{l}{xsinα+ycosβ=0}\\{xcosα-ysinβ=0}\end{array}\right.$,则α的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |