题目内容
已知曲线 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线 的参数方程是:
的参数方程是: (
( 是参数).
是参数).
(1)将曲线 和曲线
和曲线 的方程转化为普通方程;
的方程转化为普通方程;
(2)若曲线 与曲线
与曲线 相交于
相交于 两点,求证
两点,求证 ;
;
(3)设直线 交于两点
交于两点 ,且
,且 (
( 且
且 为常数),过弦
为常数),过弦 的中点
的中点 作平行于
作平行于 轴的直线交曲线
轴的直线交曲线 于点
于点 ,求证:
,求证: 的面积是定值.
的面积是定值.
(1)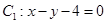 ;
;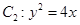 ;(2)证明详见解析;(3)证明详见解析.
;(2)证明详见解析;(3)证明详见解析.
解析试题分析:(1)先将极坐标方程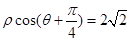 转化为
转化为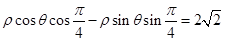 ,后由极坐标与普通方程转化的关系式
,后由极坐标与普通方程转化的关系式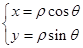 得出
得出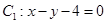 ;由
;由 消去参数
消去参数 即可得到
即可得到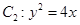 ;(2)联立方程
;(2)联立方程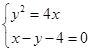 消去
消去 得到
得到 ,设
,设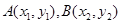 ,根据根与系数的关系得到
,根据根与系数的关系得到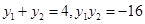 ,进而得到
,进而得到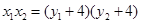 ,再检验
,再检验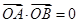 即可证明
即可证明 ;(3)联立方程
;(3)联立方程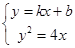 ,消
,消 得
得 ,进而得到
,进而得到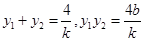 ,由
,由 得出
得出 ,进而确定
,进而确定 的坐标,最后计算
的坐标,最后计算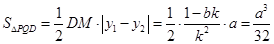 可得结论.
可得结论.
(1)由极坐标方程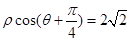 可得
可得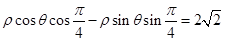
而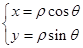 ,所以
,所以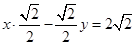 即
即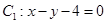
由 消去参数
消去参数 得到
得到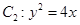
(2)设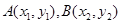 ,联立方程并消元得:
,联立方程并消元得:
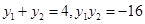 ,
,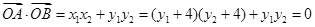
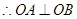
(3)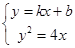 ,消
,消 得
得 ,
,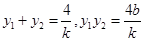
由 (
( 且
且 为常数),得
为常数),得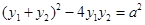
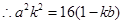 ,又可得
,又可得 中点
中点 的坐标为
的坐标为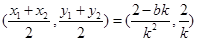
所以点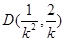 ,
,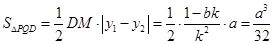 ,面积是定值.
,面积是定值.
考点:1.极坐标;2.参数方程;3.直线与抛物线的位置关系;4.三角形的面积计算公式.

练习册系列答案
相关题目
 ,M,N分别为曲线C与x轴、y轴的交点.
,M,N分别为曲线C与x轴、y轴的交点. (α为参数).
(α为参数). ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系; sin
sin ,以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系. 的圆的极坐标方程.
的圆的极坐标方程. ,点P的轨迹为曲线C.
,点P的轨迹为曲线C. 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程; 距离的最大值.
距离的最大值. 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4. .
. ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程. 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,x轴为极轴建立极坐标系得另一直线
为参数),以坐标原点为极点,x轴为极轴建立极坐标系得另一直线 的方程为
的方程为 ,
,
 ,则实数
,则实数 的值为 .
的值为 .