题目内容
如图,在四棱锥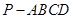 中,底面
中,底面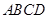 为直角梯形,且
为直角梯形,且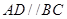 ,
,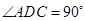 ,平面
,平面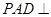 底面
底面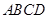 ,
,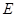 为
为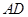 的中点,
的中点,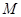 是棱
是棱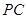 的中点,
的中点, .
.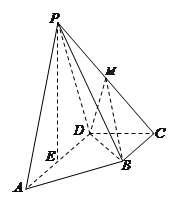

(Ⅰ)求证: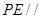 平面
平面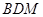 ;
;
(Ⅱ)求三棱锥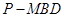 的体积.
的体积.
(Ⅰ)详见解析;(Ⅱ)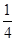 .
.
解析试题分析:(Ⅰ)本小题是一个证明线面平行的题,一般借助线面平行的判定定理求解,连接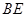 ,因为
,因为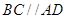 ,
,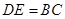 ,所以四边形
,所以四边形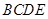 为平行四边形,连接
为平行四边形,连接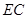 交
交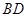 于
于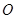 ,连接
,连接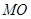 ,则
,则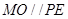 ,则根据线面平行的判定定理可知
,则根据线面平行的判定定理可知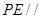 平面
平面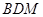 .
.
(Ⅱ)由于平面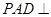 底面
底面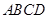 ,
,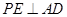 ,由面面垂直的性质定理可知
,由面面垂直的性质定理可知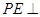 底面
底面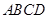 ,
,
所以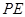 是三棱锥
是三棱锥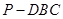 的高,且
的高,且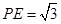 ,又因为
,又因为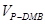 可看成
可看成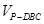 和
和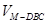 差构成,由(Ⅰ)知
差构成,由(Ⅰ)知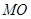 是三棱锥
是三棱锥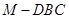 的高,
的高,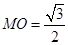 ,
,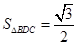 ,可知
,可知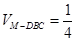 ,又由于
,又由于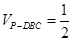 ,可知
,可知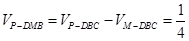 .
.
试题解析:连接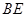 ,因为
,因为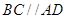 ,
,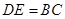 ,所以四边形
,所以四边形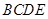 为平行四边形
为平行四边形
连接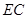 交
交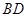 于
于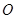 ,连接
,连接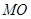 ,则
,则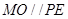 ,
,
又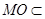 平面
平面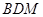 ,
,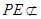 平面
平面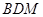 ,所以
,所以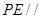 平面
平面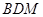 .
.
(2)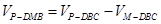 ,
,
由于平面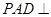 底面
底面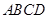 ,
,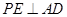
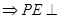 底面
底面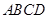
所以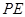 是三棱锥
是三棱锥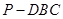 的高,且
的高,且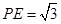
由(1)知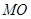 是三棱锥
是三棱锥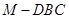 的高,
的高,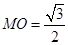 ,
,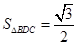 ,
,
所以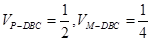 ,则
,则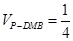 .
.
考点:1.直线与平面平行的判定;2.锥体的体积公式.

练习册系列答案
相关题目
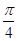 ,∠DAB=
,∠DAB=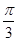 .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题: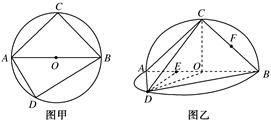
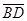 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.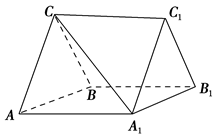
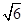 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;
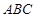 中,
中,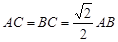 ,
,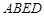 是边长为
是边长为 的正方形,平面
的正方形,平面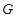 、
、 分别是
分别是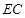 、
、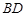 的中点.
的中点.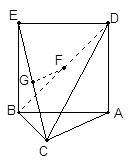
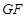 ∥底面
∥底面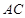 ⊥平面
⊥平面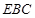 ;
;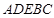 的体积.
的体积.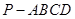 中,底面
中,底面 是菱形,
是菱形,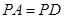 ,
,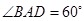 ,
,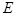 是
是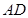 的中点,点
的中点,点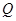 在侧棱
在侧棱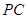 上.
上.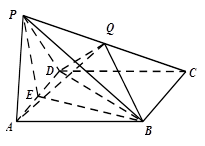
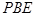 ;
; //平面
//平面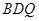 ;
;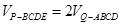 ,试求
,试求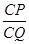 的值.
的值.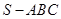 中,
中,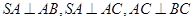 且
且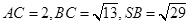 .
.
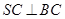 ;
;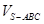 .
.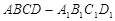 的棱长为
的棱长为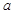 .
.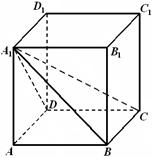
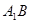 与
与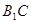 所成角的大小;
所成角的大小;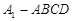 的体积.
的体积.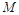 是
是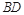 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.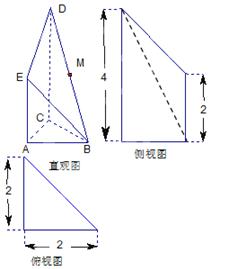
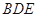 ? 若存在,确定
? 若存在,确定