题目内容
【题目】已知定点 
， 
为圆 
上任意一点，线段 
上一点 
满足 
，直线 
上一点 
，满足 
.
（1）当 在圆周上运动时，求点 
的轨迹 
的方程；
（2）若直线 
与曲线 交于 
两点，且以 
为直径的圆过原点 
，求证：直线 与 
不可能相切.
【答案】
（1）解：由 
，直线 
上一点 
，满足 
，可得 
时线段 的垂直平分线，求出圆 
的圆心坐标为 
，半径为 
，得到 
，点Q的轨迹是以F1、F2为焦点，长轴长为 
的椭圆，即2a= ，2c= 
，∴b= 
．
所以点Q的轨迹C的方程为： 
（2）解：当直线的斜率存在时，设直线l为y=kx+m ， A（x1 ， y1），B（x2 ， y2），联立直线与椭圆的方程，
得 
消去y并整理得（1+2k2）x2+4kmx+2m2-6=0．
因为直线与椭圆有两个不同的交点，所以
△=16k2m2-4（1+2k2）（2m2-6）＞0，化简得：m2＜6k2+3①
由韦达定理得： 
．
∴ 
．
∵ 
，∴x1x2+y1y2=0，即 
，
整理得m2=2k2+2满足①式，∴d= 
，即原点到直线l为的距离是 
，
∴直线l与圆x2+y2=4相交．
当直线的斜率不存在时，直线为x=m ， 与椭圆C交点为A（m ， 
），B（m ， 
）
∵ ，∴ 
．
此时直线为x= 
，显然也与圆x2+y2=4相交．
综上，直线l与定圆E：x2+y2=4不可能相切
【解析】（1）本题最重数形结合的思想，先画出草图，将数据标到图上，使题目清晰化。再根据线段长度之间的关系，得到Q点到F1 ， F2两点的距离之和为一定值，且大于F1和F2间的距离，故满足椭圆定义，可知曲线C是一椭圆，即可得到结果。
（2）先根据条件设出直线，联立消元得到一元二次方程，由相交于两点可得
；以AB为直径的圆过原点，故可得；，由以上两个条件可得k和m关系，然后用点到直线的距离公式，看原点到直线的距离是否满足证明，即距离不等于2。
【考点精析】利用点到直线的距离公式和椭圆的概念对题目进行判断即可得到答案，需要熟知点
到直线
的距离为：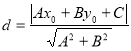
；平面内与两个定点
，
的距离之和等于常数（大于
）的点的轨迹称为椭圆,这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距．
