Question

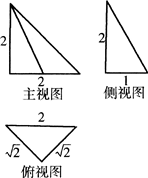（2010•朝阳区二模）下图是一个空间几何体的三视图，则该几何体的体积为

2

3

．

Answer 1

分析：由空间几何体的三视图，知该几何体是三棱锥P-ABC，其中PA⊥面ABC，且PA=AC=2，AB=BC=

2

，由此能求出该几何体的体积．

解答：解：由空间几何体的三视图，
知该几何体是如图所示的三棱锥P-ABC，
其中PA⊥面ABC，且PA=AC=2，AB=BC=

2

，
∴∠ABC=90°，
∴S△ABC=

1

2

×

2

×

2

=1，
∴该几何体的体积V=

1

3

×S△ABC×PA=

1

3

×1×2=

2

3

．
故答案为：

2

3

．

点评：本题考查由三棱锥的三视图求它的体积，是基础题．解题时要认真审题，仔细解答．