题目内容
设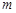 是给定的正整数,有序数组(
是给定的正整数,有序数组(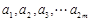 )中
)中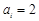 或
或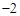
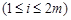 .
.
(1)求满足“对任意的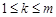 ,
,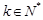 ,都有
,都有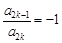 ”的有序数组(
”的有序数组(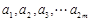 )的个数
)的个数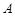 ;
;
(2)若对任意的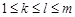 ,
,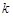 ,
,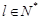 ,都有
,都有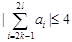 成立,求满足“存在
成立,求满足“存在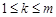 ,使得
,使得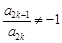 ”的有序数组(
”的有序数组(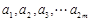 )的个数
)的个数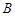 .
.
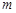 是给定的正整数,有序数组(
是给定的正整数,有序数组(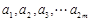 )中
)中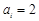 或
或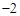
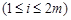 .
.(1)求满足“对任意的
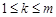 ,
,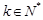 ,都有
,都有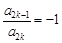 ”的有序数组(
”的有序数组(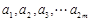 )的个数
)的个数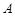 ;
;(2)若对任意的
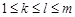 ,
,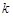 ,
,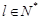 ,都有
,都有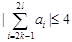 成立,求满足“存在
成立,求满足“存在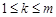 ,使得
,使得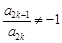 ”的有序数组(
”的有序数组(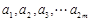 )的个数
)的个数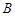 .
.(1) ,(2)
,(2) .
.
 ,(2)
,(2) .
.试题分析:
(1)正确理解每一偶数项与前相邻奇数项是相反数,而与后相邻奇数项相等或相反;因此分组按(奇、偶)分为
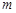 组,每组有2种可能,各组可能互不影响,共有
组,每组有2种可能,各组可能互不影响,共有 种可能,
种可能,(2)在(1)的基础上,某些组可能为(2,2)或(-2,-2),需讨论这些组个数的情况,最少一个,最多
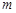 个.另外条件“对任意的
个.另外条件“对任意的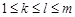 ,
,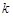 ,
,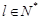 ,都有
,都有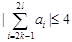 成立”控制不能出现各组都为2或-2的情况,而是间隔出现(2,2)、(-2,-2).
成立”控制不能出现各组都为2或-2的情况,而是间隔出现(2,2)、(-2,-2).试题解析:
解:(1)因为对任意的
 ,都有
,都有 ,则
,则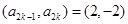 或
或
共有
 种,所以
种,所以 共有
共有 种不同的选择,所以
种不同的选择,所以 . 5分
. 5分(2)当存在一个
 时,那么这一组有
时,那么这一组有 种,其余的由(1)知有
种,其余的由(1)知有 ,所有共有
,所有共有 ;
;当存在二个
 时,因为条件对任意的
时,因为条件对任意的 ,都有
,都有 成立得这两组共有
成立得这两组共有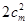 ,
,其余的由(1)知有
 ,所有共有
,所有共有 ;
;依次类推得:
 . 10分
. 10分
练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
 )5的展开式中x2项的系数是15,则展开式的所有项系数的和是________.
)5的展开式中x2项的系数是15,则展开式的所有项系数的和是________. ,在二项式
,在二项式 的展开式中,含
的展开式中,含 的项的系数与含
的项的系数与含 的项的系数相等,则
的项的系数相等,则 的值为 .
的值为 . 的展开式中,含
的展开式中,含 的项的系数是___________.
的项的系数是___________. 的展开式中常数项是 .
的展开式中常数项是 . 二项展开式中的常数项为( )
二项展开式中的常数项为( ) 的展开式中
的展开式中 的系数是-35,则
的系数是-35,则 = .
= . =
= +
+ +
+ +…+
+…+ (x∈R),则
(x∈R),则 +
+ +
+ +…+
+…+ ( )
( )
