题目内容
已知函数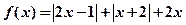 ,
,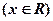
 (Ⅰ)求函数
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)已知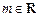 ,命题p:关于x的不等式
,命题p:关于x的不等式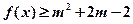 对任意
对任意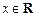 恒成立;命题
恒成立;命题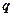 :指数函数
:指数函数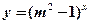 是增函数.若“p或q”为真,“p且q”为假,求实数
是增函数.若“p或q”为真,“p且q”为假,求实数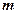 的取值范围.
的取值范围.
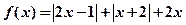 ,
,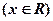
 (Ⅰ)求函数
(Ⅰ)求函数 的最小值;
的最小值;(Ⅱ)已知
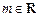 ,命题p:关于x的不等式
,命题p:关于x的不等式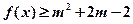 对任意
对任意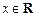 恒成立;命题
恒成立;命题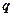 :指数函数
:指数函数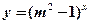 是增函数.若“p或q”为真,“p且q”为假,求实数
是增函数.若“p或q”为真,“p且q”为假,求实数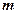 的取值范围.
的取值范围.解:(Ⅰ)由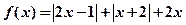 得
得
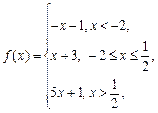 作出函数
作出函数 的图象,
的图象,
可知函数 在
在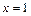 处取得最小值1.。。。。。。。。。。。。。 4分
处取得最小值1.。。。。。。。。。。。。。 4分
(Ⅱ)由(Ⅰ)得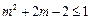 ,
,
即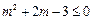 ,解得
,解得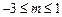 ,
,
∴命题p: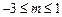 . 。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
. 。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
对于命题q,函数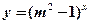 是增函数,则
是增函数,则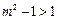 ,即
,即 ,
,
∴命题q: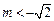 或
或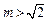 . 。。。。。。。。。。。。。。。。。。。。8分
. 。。。。。。。。。。。。。。。。。。。。8分
由“p或q”为真,“p且q”为假可知有以下两个情形:
若p真q假,则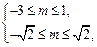 解得
解得 , 。。。。。。。。10分
, 。。。。。。。。10分
若p假q真,则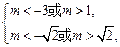 解得
解得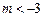 或
或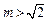 ,
,
故实数m的取值范围是 .。。。。。。。。。12分
.。。。。。。。。。12分
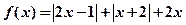 得
得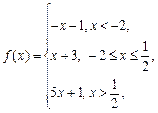 作出函数
作出函数 的图象,
的图象,可知函数
 在
在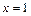 处取得最小值1.。。。。。。。。。。。。。 4分
处取得最小值1.。。。。。。。。。。。。。 4分(Ⅱ)由(Ⅰ)得
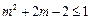 ,
,即
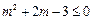 ,解得
,解得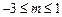 ,
,∴命题p:
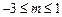 . 。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
. 。。。。。。。。。。。。。。。。。。。。。。。。。。。6分对于命题q,函数
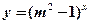 是增函数,则
是增函数,则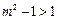 ,即
,即 ,
,∴命题q:
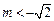 或
或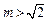 . 。。。。。。。。。。。。。。。。。。。。8分
. 。。。。。。。。。。。。。。。。。。。。8分由“p或q”为真,“p且q”为假可知有以下两个情形:
若p真q假,则
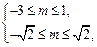 解得
解得 , 。。。。。。。。10分
, 。。。。。。。。10分若p假q真,则
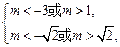 解得
解得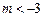 或
或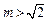 ,
,故实数m的取值范围是
 .。。。。。。。。。12分
.。。。。。。。。。12分略

练习册系列答案
相关题目
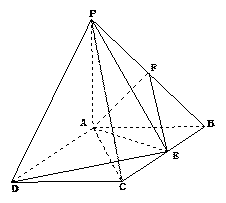
 ,则正四面体上的所有点在平面
,则正四面体上的所有点在平面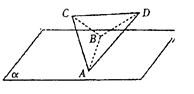
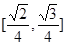
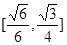
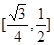
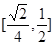
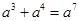
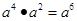
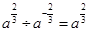
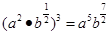
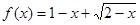 的值域为( )
的值域为( )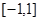
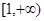

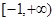
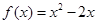 ,
,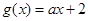 (
(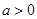 ),若
),若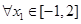 ,
,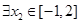 ,使得
,使得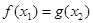 ,则实数
,则实数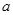 的取值范围是
的取值范围是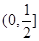
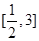
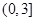
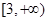

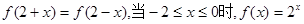 ,
,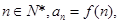 则
则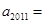 ( )
( ) 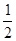
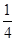
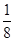
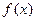 是
是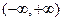 上的偶函数,若对于
上的偶函数,若对于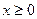 ,都有
,都有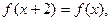
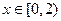 时,
时,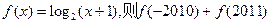 的值为( )
的值为( )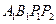 的顶点
的顶点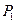 、
、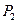 在反比例函数
在反比例函数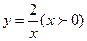 的图象上,顶点
的图象上,顶点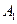 、
、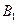 分别在
分别在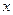 轴、
轴、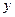 轴的正半轴上,再在其右侧作正方形
轴的正半轴上,再在其右侧作正方形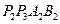 ,顶点
,顶点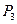 、
、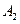 在
在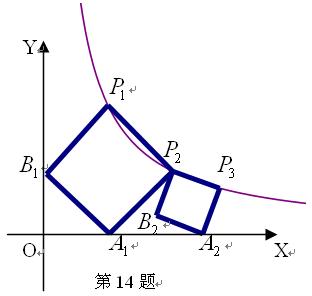
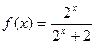 ,则
,则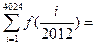 .
.