题目内容
已知双曲线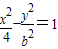 的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
【答案】分析:可求得抛物线y2=12x的焦点坐标,从而可求得b2及双曲线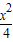 -
-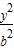 =1的右焦点坐标,利用点到直线间的距离公式即可.
=1的右焦点坐标,利用点到直线间的距离公式即可.
解答:解:∵抛物线y2=12x的焦点坐标为(3,0),
依题意,4+b2=9,
∴b2=5.
∴双曲线的方程为: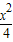 -
-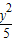 =1,
=1,
∴其渐近线方程为:y=±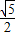 x,
x,
∴双曲线的一个焦点F(3,0)到其渐近线的距离等于d=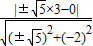 =
=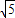 .
.
故答案为: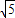 .
.
点评:本题考查双曲线的简单性质,求得b2的值是关键,考查点到直线间的距离公式,属于中档题.
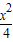 -
-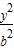 =1的右焦点坐标,利用点到直线间的距离公式即可.
=1的右焦点坐标,利用点到直线间的距离公式即可.解答:解:∵抛物线y2=12x的焦点坐标为(3,0),
依题意,4+b2=9,
∴b2=5.
∴双曲线的方程为:
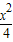 -
-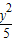 =1,
=1,∴其渐近线方程为:y=±
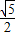 x,
x,∴双曲线的一个焦点F(3,0)到其渐近线的距离等于d=
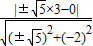 =
=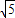 .
.故答案为:
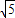 .
.点评:本题考查双曲线的简单性质,求得b2的值是关键,考查点到直线间的距离公式,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则该双曲线的焦点到其渐近线的距离等于
.
的焦点重合,则该双曲线的焦点到其渐近线的距离等于
. 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则该双曲线的离心率为 ( )
的焦点重合,则该双曲线的离心率为 ( ) B.
B. C.
C. D.
D.

 的右焦点与抛物线
的右焦点与抛物线 焦点重合,则此双曲线的渐近线方程是(
)
焦点重合,则此双曲线的渐近线方程是(
) B.
B. C.
C. D.
D.