题目内容
(2004•朝阳区一模)已知动双曲线的右顶点在抛物线y2=x-1上,实轴长为定值4,右准线恰为y轴.
(Ⅰ)求动双曲线中心的轨迹方程;
(Ⅱ)求虚半轴长的取值范围.
(Ⅰ)求动双曲线中心的轨迹方程;
(Ⅱ)求虚半轴长的取值范围.
分析:(I)设设双曲线的中心为M(x,y),由于右准线为y轴,故x<0.再根据实轴长为4,得双曲线的右顶点为(x+2,y).由题意知点(x+2,y)在抛物线y2=x-1上,由此能求出动双曲线中心的轨迹方程.
(Ⅱ)先设双曲线方程为
-
=1(a>0,b>0).可得右准线为x=x0+
.而右准线方程为x=0,从而有x0=-
=-
.由(Ⅰ)知
=x0+1,故
=-
+1≥0.由此建立关于b的不等关系即可求出虚半轴长的取值范围.
(Ⅱ)先设双曲线方程为
| (x-x0)2 |
| a2 |
| (y-y0)2 |
| b2 |
| a2 |
| c |
| a2 |
| c |
| 4 | ||
|
| y | 2 0 |
| y | 2 0 |
| 4 | ||
|
解答:解:(Ⅰ):设双曲线的中心为(x,y),由于右准线为y轴,故x<0.
∵实轴长为4,故a=2.
∴双曲线的右顶点为(x+2,y).
由题意知点(x+2,y)在抛物线y2=x-1上,
∴y2=(x+2)-1=x+1.
∴双曲线中心的轨迹方程为y2=x+1(-1≤x<0).…(6分)
(Ⅱ):设双曲线方程为
-
=1(a>0,b>0).
∵a=2,故c=
.
由x-x0=
,得右准线为x=x0+
.
而右准线方程为x=0,
∴x0+
=0.
∴x0=-
=-
.
由(Ⅰ)知
=x0+1,
故
=-
+1≥0.
化简得b2≥12,故b≥2
.
∴虚半轴长的取值范围是[2
,+∞).…(14分)
∵实轴长为4,故a=2.
∴双曲线的右顶点为(x+2,y).
由题意知点(x+2,y)在抛物线y2=x-1上,
∴y2=(x+2)-1=x+1.
∴双曲线中心的轨迹方程为y2=x+1(-1≤x<0).…(6分)
(Ⅱ):设双曲线方程为
| (x-x0)2 |
| a2 |
| (y-y0)2 |
| b2 |
∵a=2,故c=
| a2+b2 |
由x-x0=
| a2 |
| c |
| a2 |
| c |
而右准线方程为x=0,
∴x0+
| a2 |
| c |
∴x0=-
| a2 |
| c |
| 4 | ||
|
由(Ⅰ)知
| y | 2 0 |
故
| y | 2 0 |
| 4 | ||
|
化简得b2≥12,故b≥2
| 3 |
∴虚半轴长的取值范围是[2
| 3 |
点评:本题主要考查抛物线标准方程,双曲线的简单几何性质等基础知识.考查运算求解能力,推理论证能力,考查化归与转化思想.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
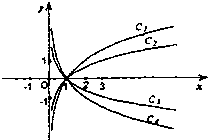 (2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )
(2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )