题目内容
已知a＞b≥2，有下列不等式：①b2＞3b-a；②
；③ab＞a+b；④loga3＞logb3；其中正确的是
- A.②④
- B.①②
- C.③④
- D.①③
D
分析：用作差法比较可得①③正确，通过给变量取特殊值检验可得②④不正确．
解答：∵a＞b≥2，
∴b2 -3b+a=（a-b）+b（b-2）＞0+0=0，故①正确．
不正确，例如 a=10，b=2时，左边为 
，右边也为，故②不正确．
ab-（a+b ）=
=
＞
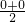=0，故③正确．
④不正确，如a=9，b=3 时，左边为
，右边为1，显然不等式不成立．
综上，只有①③正确，
故选D．
点评：本题考查比较两个式子大小的方法，通过给变量取特殊值，举反例来说明某个命题不正确，是一种简单有效的方法．
分析：用作差法比较可得①③正确，通过给变量取特殊值检验可得②④不正确．
解答：∵a＞b≥2，
∴b2 -3b+a=（a-b）+b（b-2）＞0+0=0，故①正确．
不正确，例如 a=10，b=2时，左边为 ，右边也为，故②不正确．ab-（a+b ）=
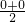=＞=0，故③正确．④不正确，如a=9，b=3 时，左边为
，右边为1，显然不等式不成立．综上，只有①③正确，
故选D．
点评：本题考查比较两个式子大小的方法，通过给变量取特殊值，举反例来说明某个命题不正确，是一种简单有效的方法．
练习册系列答案
相关题目
A．选修4-1：几何证明选讲
本题有（1），（2），（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑．