题目内容
已知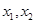 是函数
是函数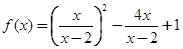 的两个零点,则
的两个零点,则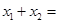
A. | B. | C.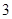 | D. |
B
解析试题分析:令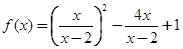 =0,整理得:
=0,整理得: ,由韦达定理得
,由韦达定理得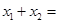 2,故选B。
2,故选B。
考点:本题主要考查零点的概念,代数式恒等变形,韦达定理的应用。
点评:简单题,函数的零点即函数值为0时,对应x的值。

练习册系列答案
相关题目
已知 ,
, ,则有:( )
,则有:( )
A. | B. |
C. | D.以上都不是 |
设奇函数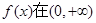 上为减函数,且
上为减函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
下列各组函数是同一函数的是( )
①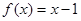 与
与 ; ②
; ②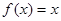 与
与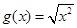 ;
;
③ 与
与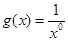 ; ④
; ④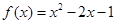 与
与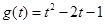 。
。
| A.①② | B.①③ | C.③④ | D.①④ |
已知定义域为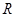 的函数
的函数 满足
满足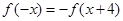 ,则
,则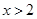 时,
时, 单调递增,若
单调递增,若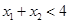 ,且
,且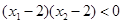 ,则
,则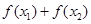 与0的大小关系是( )
与0的大小关系是( )
A.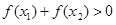 | B.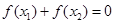 |
C. | D.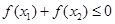 |
函数 的零点所在的区间为( )
的零点所在的区间为( )
A. | B. | C. | D. |
设函数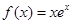 ,则( )
,则( )
A.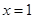 为 为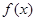 的极大值点 的极大值点 | B.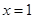 为 为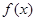 的极小值点 的极小值点 |
C.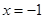 为 为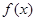 的极大值点 的极大值点 | D.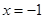 为 为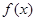 的极小值点 的极小值点 |
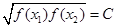 ,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为
,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为 B.2 C.4 D. 2
B.2 C.4 D. 2 的图象的是
的图象的是