题目内容
 在平面直角坐标系xOy中,已知四边形OABC是平行四边形,且点
在平面直角坐标系xOy中,已知四边形OABC是平行四边形,且点 .
.
(1)求∠ABC的大小;
(2)设点M是OA的中点,点P在线段BC上运动
(包括端点),求 的取值范围.
的取值范围.
解:(1)由题意得 ,
,
因为四边形OABC是平行四边形,
所以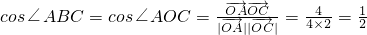 .
.
于是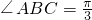 .
.
(2)设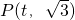 ,其中1≤t≤5.
,其中1≤t≤5.
于是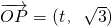 ,而
,而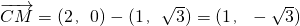 ,
,
所以 =
=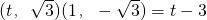 .
.
故 的取值范围是[-2,2].
的取值范围是[-2,2].
分析:(1)利用向量坐标的求法,求出边OA,OC对应的向量的坐标,利用向量的数量积公式求出∠AOC,根据平行四边形的对角相等,得到∠ABC的大小.
(2)根据p在平行于x轴的边上,设出其坐标,求出线段OP,CM对应的向量的坐标,利用向量的数量积公式求出 ,根据一次函数的单调性求出取值范围.
,根据一次函数的单调性求出取值范围.
点评:求两个向量的夹角问题,一般先利用向量数量积的坐标形式的公式求出两个向量的数量积,再利用数量积的模、夹角形式求出夹角余弦,注意向量夹角的范围,求出向量的夹角.
 ,
,因为四边形OABC是平行四边形,
所以
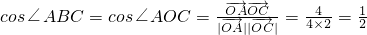 .
.于是
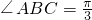 .
.(2)设
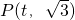 ,其中1≤t≤5.
,其中1≤t≤5.于是
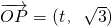 ,而
,而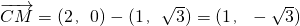 ,
,所以
 =
=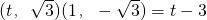 .
.故
 的取值范围是[-2,2].
的取值范围是[-2,2].分析:(1)利用向量坐标的求法,求出边OA,OC对应的向量的坐标,利用向量的数量积公式求出∠AOC,根据平行四边形的对角相等,得到∠ABC的大小.
(2)根据p在平行于x轴的边上,设出其坐标,求出线段OP,CM对应的向量的坐标,利用向量的数量积公式求出
 ,根据一次函数的单调性求出取值范围.
,根据一次函数的单调性求出取值范围.点评:求两个向量的夹角问题,一般先利用向量数量积的坐标形式的公式求出两个向量的数量积,再利用数量积的模、夹角形式求出夹角余弦,注意向量夹角的范围,求出向量的夹角.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.