Question

已知定义在[1，+∞）上的函数f（x）=

4 -|8x-12|， 1≤x≤2 1 2 f( x 2 )， x＞2

，则（　　）

• A、函数f（x）的值域为[1，4]
• B、关于x的方程f（x）-

  1

  2n

  =0（n∈N^*）有2n+4个不相等的实数根
• C、当x∈[2，4]时，函数f（x）的图象与x轴围成的面积为2
• D、存在实数x₀，使得不等式x₀f（x₀）＞6成立

Answer 1

分析：由函数的解析式作出函数的图象，利用数形结合分别进行判断即可．

解答：解：作出函数f（x）的图象如图：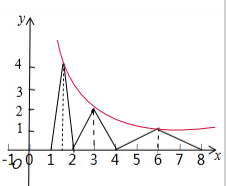
A．则当x=1时，f（1）=0，∴函数的值域为[0，4]，故A错误．
B．当n=1时，由f（x）-

1

2n

=0得f（x）=

1

2

，
∵f（12）=

1

2

f（6）=

1

2

，则f（x）=

1

2

有7个不同的根，故B错误．
C．当x∈[1，2]时，函数f（x）的图象与x轴围成的图形的面积为S，则S=

1

2

×1×4=2，故C正确；
D．由xf（x）＞6得f(x)＞

6

x

，画出函数y=

6

x

的图象，可知y=

6

x

与函数y=f（x）有交点，
如x=

3

2

，3，6等，因此不存在x₀，使得不等式即x₀f（x₀）＞6成立，故D错误．
综上可知：C正确．
故选：C

点评：本题主要考查函数图象和性质的判断，利用数形结合是解决本题的关键，综合性较强，难度较大．