题目内容
1996年诺贝尔化学奖授予对发现C60有重大贡献的三位科学家.C60分子是形如球状的多面体,如图所示.该结构的建立基于以下考虑:(1)C60分子中每个碳原子只跟相邻的3个碳原子形成化学键;(2)C60分子只含有五边形和六边形;(3)多面体的顶点数、面数和棱数的关系遵循欧拉定理:顶点数+面数-棱边数=2.据以上所述,可推知C60分子有12个五边形和20个六边形,C60分子所含的双键数为30,请回答以下问题:
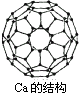
(1)固体C60与金刚石相比较,熔点较高者应是________,理由是________.
(2)试估计C60跟F2在一定条件下能否发生反应生成C60F60(填“可能”或“不可能”)________,并简述其理由________.
(3)通过计算确定C60分子所含单键数为________.
(4)C70分子也已制得,它的分子结构模型可以与C60同样考虑而推知,通过计算确定C70分子中五边形和六边形的数目.
解析:
|
解答: (1)金刚石.由于金刚石是原子晶体而固体C60为分子晶体,金刚石的熔点一定比分子晶体的熔点要高. (2)可能.C60分子有30个双键,与30个F2加成可得C60F60. (3)60. (4)设C70分子中五边形数为x,六边形数为y,依题意可得: 解之得:x=12,y=25.故五边形为12,六边形为25. 分析: 该试题分四步设问,第(1)、(2)问较为简单,由题干知识“C60分子所含双键数为30”,可知C60为分子晶体,可发生加成反应,最多加成30个F2.而后两问难度逐渐加大,有很好的区分度,是今后考试命题趋向. 如果将化学问题抽象成数学问题,解法要简单的多.将碳原子数抽象为球状多面体的顶点数,碳原子间的共价键数(包括单、双键)看作棱边数,C原子形成的五元环和六元环数为面数.由欧拉定理可算出共价键总数为:60+(12+20)-2=90,故C60分子内单键数为:90-30=60. 借助几何体的顶点数与棱边数的关系求化学键总数更简便:因为顶点数为60,且每个顶点连线三条边,每条边又有两个顶点,则每个顶点占每条边的1/2,所以C60分子的边数(化学键总数)为:60×3×1/2=90. 还可以借助几何体的面数与边数的关系求化学键总数:C60分子共有12个五边形,20个六边形,其中每条边为两个面共用,所以边数共有:(12×5+20×6)× 也可由碳原子成键规律直接求单键数:因为C60分子中跟相邻的3个碳原子形成化学键,而碳原子又必须是4个价键,所以每个碳原子只含一个双键,两个单键,故单键数为双键数的2倍,所以单键数为:30×2=60. C70分子中五边形和六边形数目可列方程组求解. |

 阅读快车系列答案
阅读快车系列答案| A、C60与棒碳中所有的化学键都是非极性共价键 | B、棒碳不能使溴水褪色 | C、C60在一定条件下可能与CuO发生置换反应 | D、棒碳与乙炔互为同系物 |
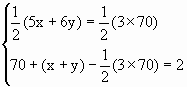



 法正确的是 ( )
法正确的是 ( )