Question

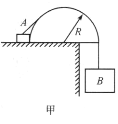
【题目】在跳台边缘固定一个半径为R的半圆形光滑柱面，一根不可伸长的细绳两端分别系物体A和B，且，如图甲所示，现从图示位置开始，由静止释放B物体。

（1）试证明A物体在到达圆柱面的最高点前，就离开圆柱面。

（2）A物体离开圆柱面时，求转过的角度变量与其他已知量之间的关系。

（3）若A物体刚好能达到最高点，求和的比值应满足的关系。

Answer 1

【答案】（1）A不能到达最高点，应在到达最高点之前A就离开圆柱面。（2） （3）且A恰能通过最高点，需满足，代入上式得：时，A在到达最高点之前脱离； 时，A可以顺利通过最高点。

【解析】

（1）若A能到达最高点，则

，

又，

解得。

A在最高点时的向心力为

。

A在最高点实际能提供的最大向心力为，因为，

所以A不能到达最高点，应在到达最高点之前A就离开圆柱面。

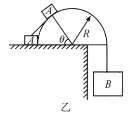
（2）设A在某一位置处离开柱面，如图乙所示，则

，

。

A离开柱面时不受柱面作用力，只有重力的径向分力提供向心力，所以

，

即有。

（3）若A能到达最高点，则

，

且A恰能通过最高点，需满足，代入上式得

，

即时，A在到达最高点之前脱离；

时，A可以顺利通过最高点。