题目内容
【题目】音叉
做匀速圆周运动，其角速度为
，圆的半径为
，音叉的频率为
，空气中声速为
，静止的接收器
与音叉做圆周运动的圆周共面，距圆心
的距离为
.设
与
的夹角为
，试问：当接收器收到声波频率为最大时，该时刻为多少？并求出最大频率.
【答案】
【解析】
当声源以速度
沿与声源和观测者的连线成
角运动时，观测者接收到的频率
与声源的频率
之间满足
.
由此可知，当为0时，有最大值为
.
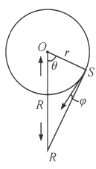
由几何关系知，此时
，当波从
传到
处时，有
.
故当
时，接收频率
最大，为
.
对于波源与观察者在它们的连线上运动的多普勒现象的研究，学生们应是非常熟悉的，但对它们不在其连线方向上运动的情况，一般资料上并没有直接的公式，而本题的解答直接运用了相关结论，严格地说，不太妥当，这种解答呈现出试卷上，可能会导致失分，正确的做法是将相关的结论推导一遍.本题实质上也给了我们一个提示，对于波源与观察者的运动不在它们连线上的多普勒现象，也是存在相关公式的，我们不妨在学习过程中推导一下.
练习册系列答案
阅读快车系列答案
相关题目
