题目内容
【题目】—根不可伸长的细轻绳，穿上一粒质量为m的珠子（视为质点），绳的下端固定在A点，上端系在轻质小环上，小环可沿固定的水平细杆滑动（小环的质量及与细杆摩擦皆可忽略不计）。细杆与A在同一竖直平面内。开始时，珠子紧靠小环，绳被拉直，如图所示。已知：绳长为L，A点到杆的距离为h，绳能承受的最大张力为
，珠子下滑过程中到达最低点前绳子被拉断。求细绳被拉直时珠子的位置和速度的大小（珠子与绳子之间无摩擦）。
【答案】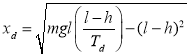
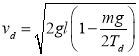
【解析】
（1）珠子运动的轨迹
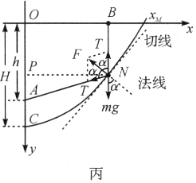
建立如图丙所示的坐标系，原点
在过
点的竖直线与细杆相交处，
轴沿细杆向右，
轴沿
向下. 当珠子运动到
点且绳子未断时，小环在
处，
垂直于轴，所以珠子的坐标为
，
.
由
知
，即有
，得
. ①
这是一个以轴为对称轴，顶点位于
处，焦点与顶点的距离为
的抛物线，如图丙所示，图中的
，为焦点.
（2）珠子在点的运动方程
因为忽略绳子的质量，所以可把与珠子接触的那一小段绳子看作是珠子的一部分，则珠子受的力有三个，一是重力
；另外两个是两绳子对珠子的拉力，它们分别沿
和
方向，这两个拉力大小相等，皆用
表示，则它们的舍力的大小为
， ②
为点两边绳子之间夹角的一半，
沿
的角平分线方向.
因为
是焦点至的连线，平行于轴，根据解析几何所述的抛物线性质可知，点的法线是的角平分线. 故合力的方向与点的法线一致.
由以上的论证，再根据牛顿运动定律和题中的注，珠子在点的运动方程（沿法线方向）应为
，
即
.③
式中
是点处轨道曲线的曲率半径；
为珠子在处时速度的大小. 根据机械能守恒定律可得
.④
（3）.求曲率半径
当绳子断裂时，
，由③式可见，如果我们能另想其他办法求得曲率半径与的关系，则就可能由③④两式求得绳子断裂时珠子的纵坐标. 现提出如下一种办法．做一条与小珠轨迹对于轴呈对称状态的抛物线，如图丁所示. 由此很容易想到这是一个从高
处平抛物体的轨迹. 平抛运动是我们熟悉的，我们不仅知道其轨迹是抛物线，而且知道其受力情况及详细的运动学方程，这样我们可不必通过轨道方程而是运用力学原理分析其运动过程，即可求出与对称的
点处抛物线的曲率半径与的关系，也就是处抛物线的曲率半径与的关系.
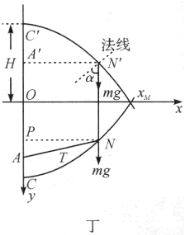
设从抛出至落地的时间为
，则有
.
由此解得
.⑤
设物体在处的速度为
，由机械能守恒定律可得
.⑥
物体在处法线方向的运动方程为
⑦
式中即为处抛物线的曲率半径，从⑤⑥⑦式及，可求得
.
这也等于点抛物线的曲率半径，
，故得
⑧
4.求绳被拉断时小珠的位置和速度的大小
把④⑧式代入③式，可求得绳子的张力为
.⑨
当时，绳子被拉断，设此时珠子位置的坐标为
，由⑨式得
.
代入①式，得
.
绳子断开时，珠子速度的大小为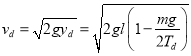
.
