题目内容
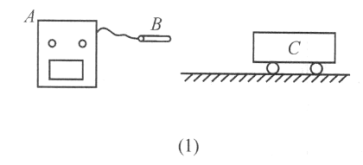
【题目】如图所示，
，是若干正方形导线方格
，
，
，…，
构成的网络，方格每边长度
.边
，
，，
，…与边
，
，
，…的电阻都等于
，边
，
，
，…的电阻都等于
.已知两点间的总电阻为
，
是已知数.在
的半空间分布有随时间
均匀增加的匀强磁场，磁场方向垂直于
平面并指向纸内.今令导线网络以恒定的速度
沿
方向运动并进入磁场区域，在运动过程中方格的边始终与
轴平行.若取与重合的时刻为
，在以后任一刻，磁场的磁感应强度为
，式中的单位为
，
为已知恒量，
.求
时刻，通过导线的电流强度（忽略导线网络的自感）.
【答案】
【解析】
网络由
个方格构成.用
表示
两端的总电阻，则
.
设
左边的所有网格（包括）的总电阻为
，则可求得
.
由此得
.
同理可得
.
在网络沿
方向运动的过程中，因为导线切割磁感应线和磁场随时间变化，都可以在导线中产生感应电动势.每一个完整的方格通过
轴所经历的时间为
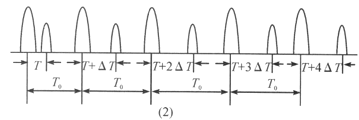
；在
时，有一个完整的方格已在磁场区域中，此时网络在磁场中的位置如图乙所示.
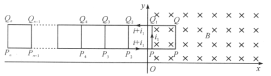
乙
设有关导线中的电流如图乙所示，令
中的感应电动势为
，则有
.
若方格
中的感应电动势为
，则有
.
由于方格全部都在磁场中，与因切割磁感线而产生的感应电动势之和为零，仅是因为磁场随时间的变化而引起的，即有
.
方格的
尚未进入磁场，故中的一部分是因在磁场中的运动而产生的感应电动势，即
.
另一部分则是由磁场的变化引起的感应电动势，即
.
.
解上述各式得
.
将已知量及
代入上式得
.
本题是第15届全国中学生物理竞赛复赛试题.
命题人将复杂的网络结构与导线切割磁感应线和磁场随时间变化产生的电动势结合起来，在试场中理清这些量间的关系，都不是一般答题者能够完成的.
答题过程中，若能敏锐地将磁场外的线框整体处理，能大大地简化电路结构与电路的分析、计算过程，若不能做到这一点，解答便不能前行，可见，解题时的全局观念，解题过程中整体法与隔离法的应用对我们完成解答是极为重要的.
