Question

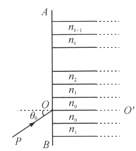
【题目】有一块透明的光学材料，由折射率略有不同的许多相互平行，厚度为的薄层密接构成，下图所示为与各薄层垂直的一个截面，AB为此材料的端面，与薄层界面垂直。表示截面的中心线。各薄层的折射率数值为，其中，。今有一光线PO以入射角射向Ο点，求此光线在材料内能够到达的离最远的距离。

Answer 1

【答案】

【解析】

令光线进入材料后的折射角为（见图乙），则有

。①

此光线射至薄层1时，入射角为，设光线进入薄层1后与的夹角为，则有

,

依次逐层考虑，可得

常量。②

式中为薄层k中光线与中心线的夹角。已知，，，即随序号k的增大而减小，故随k的增大而增大，随k的增大而减小。满足②式的各值中最接近于1的那个值所对应的k即光线能进入最远的薄层的序号。在这薄层的上表面将发生全反射，光线返回，经逐层折射进入材料的下半部，到达第k层后又被反射回去，来回传播，因此，需要求出能满足

③

的k的最大值。

由①式得，

代入③式，化简得，

代入数值得。

取小于36.52的最大整数，得。

k层上表面即光线能到达的离最远处，它与的距离为

。

在特殊情况下，即恰等于某整数时，光线由层进入层时光线即与平行，故层的上表面即为光线能达到之最远处。这时有

。