Question

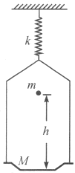
【题目】如图所示，在弹性系数为的轻质弹簧下面悬挂一个质量为的盘，盘不动时，一个质量为的质点从高处自由下落，落到盘中时与盘发生完全非弹性碰撞.此后，盘（和质点）的振动将在竖直方向振动.试求：（1）这个振动的振幅；

（2）以质点碰撞盘为计时起点、向下为位移正方向，求解振动方程.

Answer 1

【答案】（1）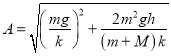

（2）

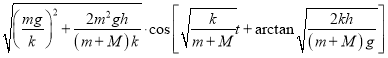
【解析】

（1）与碰撞前，的速度大小为

.

设与碰撞后的共同速度为，由动量守恒有，

所以，.

由平衡条件易知，碰撞点在新的平衡点上方，即.

设系统振动的振幅为，由能量关系有

，

可求得振幅.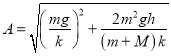

（2）系统做简谐振动，其角频率，建立平衡位置为原点且向下为正方向的坐标系，设其振动初位相为，则

，

.

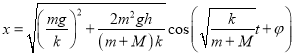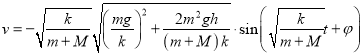将振动位移方程的初始条件

，，

代入，有

，

.

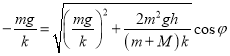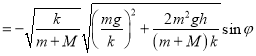所以有，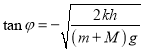

即.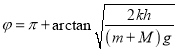

进而有

.

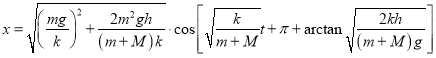
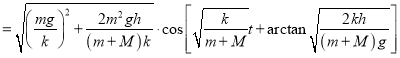对于简谐振动的分析与计算，初态的分析与计算是一个非常重要的节点，它在一定程度上决定了你对整个振动的描述正确与否.

对于初态的确定，其初位相的确定是最为复杂的，也是非常重要的，特别是在非完整的谐振中，相位的确定直接决定了解答能否进行.而相位的确定往往必须结合位移与速度进行综合判断，单一从速度与位移通常是难以确定的.

对相位的确定，既可从振动方程得到（如本题），也可利用参考圆进行确定，方法无所谓优劣，重在你处理时的谨慎与否.