题目内容
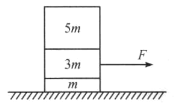
【题目】在光滑水平板上放着一块质量为
的板，板上叠放着一个斜面体和一个物体（如图所示），斜面体和物体的质量分别为
和
，斜面体斜面的倾角为
。已知和之间的动摩擦因数为
，和之间的动摩擦因数为
，现用一个水平恒力F作用在上。问：F为多大时，三个物体可保持相对静止？
【答案】（1）
时，三物体不能保持相对静止
（2）
时，F的范围是：
（3）
，F的范围是：
，且当
，亦即
时，上述的（2）、（3）又变为：
（4）
，F的范围是：
（5），F的范围是：
【解析】
当三个物体间无相对滑动时，将三个物体看作整体，有
.
显然，要求作用力
，即要求整体运动的加速度.
若
、
间无滑动，则要保证和
间无滑动，则系统最大的加速度为
，
即
.
若、间无滑动，要保证和间无滑动，则系统存在两种极端情况，即刚好不下滑和刚好不上滑两种情况，下面先求出这两种情况所对应的加速度值.
以为参照系，不相对滑动，则的受力满足
， ①
， ②
且
. ③
整理上述三式可得
，
. ④
联立①④两式可得
，且
.
显然，要确定的取值范围，需要比较
、
、
的大小，而
是明显的，为了方便，我们不妨在数轴上说明其大小关系.
先设、在数轴上的位置如图乙所示，此时
，即
，亦即
.
（1）若
，即，则三物体不能保持相对静止；
（2）若
，即
，则的范围是
.
（3）若
，即，则的范围是
.
而当
，即，亦即时，上述的（2）（3）又变为
（4），的范围是
.
（5），的范围是
.
本题是一道多对象，多临界状态的试题. 这类试题的解答，需要答题者在多个条件下进行比较、筛选，难度都比较大.
在本题所含的临界状态分析中，不仅仅是摩擦力的临界问题，同时还包含了从结论的表达式中挖掘处隐含着的临界问题，如题中
的取值范围的确定.
本题的解答采用了数轴划分区间的处理方式，体现了对数学知识运用的能力.
对于表达式类的结果，如果式中含有根式、正弦或余弦、对数、分式的分母中可能出现零的情况，都意味着我们应该对表达式产生的结果进行讨论，这里面既有临界问题的分析，更有状态质变的可能，这类情况普遍存在于各类试题中.
