Question

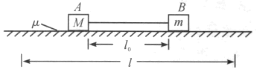
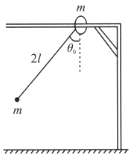
【题目】如图所示，质量可忽略、长为的细绳下端连接一质量为的小球，上端连接质量同为的小圆环，圆环套在水平的长梁上，相互间无摩擦.开始时细绳与竖直方向的夹角为，（未必为小角度），小球和环均静止，而后它们将做自由摆动.将此摆的周期记为，将另一个长为、上端固定、最大幅角也为的单摆周期记为，试比较与的大小关系.

Answer 1

【答案】

【解析】

设轻绳与竖直线夹角为时，小线水平方向速度为，竖直方向速度为，因系统水平方向动量守恒，圆环水平方向速度为，轻绳中点无水平方向运动，竖直方向速度必为，如图乙所示.

根据系统机械能守恒，有

.

小球相对点做半径为的圆运动，相对速度的两个分量为

，.

如图所示

、间有角关联：.

即得.

代入能量式，可解得.

小球相对点的摆动速度为

.

摆长为、幅角也为的单摆摆球，在摆角为时的摆动速度易求得，为

.

此表述式与是否为小角度无关.对于角范围有

，.

除了与之外，均有

.

据此即可得.

首先应注意到，此处的摆角并不一定为小角，切不可直接套用单摆的周期公式来计算相关的时间.

本题所采用的在同一角位置处比较两摆的速度大小，进而比较出运动周期的大小的分析方法在物理分析中有广泛的用途，这一方法统称为速度分析法.

速度分析法也不仅仅用于时间分析，但凡与速度相关的问题，在存在时间的比较与临界问题时，便有可能用到此法.