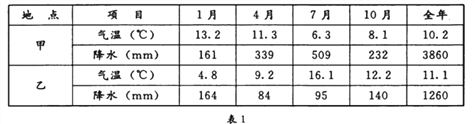
题目内容
【题目】静止于太空惯性系S的飞船,主体质量为![]() ,携带的燃料质量为
,携带的燃料质量为![]() ,某时刻发动机点火使飞船开始沿直线方向朝前加速运动,已知单位时间燃烧的燃料质量为
,某时刻发动机点火使飞船开始沿直线方向朝前加速运动,已知单位时间燃烧的燃料质量为![]() ,燃料全部生成物的喷射速度(生成物相对飞船的朝后速度)为常量u,在一直到燃料烧尽的全过程中,试求:
,燃料全部生成物的喷射速度(生成物相对飞船的朝后速度)为常量u,在一直到燃料烧尽的全过程中,试求:
(1)飞船加速度的最小值![]() 和最大值
和最大值![]() 。
。
(2)飞船末速度![]() 。
。
(3)初始时刻飞船发动机提供的功率(单位时间燃料在燃烧过程中释放的内能,即单位时间内系统动能的增量)![]() 和全过程时间内的平均功率
和全过程时间内的平均功率![]() 。
。
(4)发射效率(飞船最终获得的动能占发动机释放的全部燃料内能之比)![]() 。
。
(5)![]() 为何值(给出1位有效数字)时,
为何值(给出1位有效数字)时,![]() 取极大值?
取极大值?
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)
(3)![]() ,
,![]() 。
。
(4)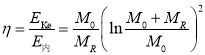 (5)
(5)![]()
【解析】
(1)t时刻飞船(主体与剩余燃料)的质量记为M,速度记为v,经![]() 时间燃烧掉燃枓质量-
时间燃烧掉燃枓质量-![]() ,飞船速度增为
,飞船速度增为![]() 。
。
由动量守恒方程有
![]() (略去二阶小量),
(略去二阶小量),
得![]() 。 ①
。 ①
将![]() ,
,![]() 代入,得
代入,得
![]() 。
。
又![]() ,
,
即有![]() ,
,![]() 时;
时;
![]() ,
,![]() 时。
时。
(2)对①式积分得
![]() ,
,
得![]() 。
。
末速度为![]() 。
。
(3)在![]() 时间内,
时间内,
![]() ,
,
系统动能增量为
![]() (略去二阶小量),
(略去二阶小量),
得![]() 。
。
将![]() 代入,得
代入,得
![]() 。
。
![]() 时间内燃料释放的内能等于系统动能的增量
时间内燃料释放的内能等于系统动能的增量![]() ,即得t时刻发动机提供的功率为
,即得t时刻发动机提供的功率为
![]() 。
。
因![]() 为常量,故
为常量,故
![]() ,
,![]() 。
。
(4)据(2)问,飞船最终获得的动能为
 。
。
释放的全部燃料内能为
![]() 。
。
所求效率便为
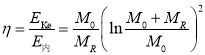 。
。
(5)将![]() 代入上式,得
代入上式,得
![]() 。
。
令![]() ,得方程
,得方程
![]() 。
。
该方程的解即对应于![]() 的极值,解的数值计算见下表:
的极值,解的数值计算见下表:
| 1 | 2 | 3 | 3.5 | 4 | 4.5 | 6 |
| 1 | 1.33 | 1.5 | 1.56 | 1.6 | 1.64 | 1.67 |
| 0.69 | 1.10 | 1.39 | 1.50 | 1.61 | 1.70 | 1.79 |
| 48% | 60% | 64% | 64.6% | 65% | 64.6% | 64% |
由此可见,![]() 时,
时,![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目