题目内容
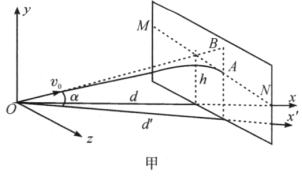
【题目】如图甲所示，一人做射靶游戏，为使每次枪弹都击中在靶面的同一条水平线上，则每次射击的瞄准点必须在靶面同一圆周上，试加以证明。（已知水平线离地面高度为h，枪与靶相距为d，子弹发射速率为
）
【答案】见解析
【解析】
如图乙（此图在题图的基础上转换了一个方位）建立坐标系，O点为子弹发射点，
轴垂直墙面（yz平面），轴与墙交于点
。
，y轴竖直向上，z轴与墙面平行，并水平指向。
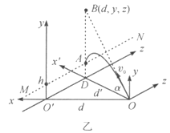
抛体运动原本是在通过抛射点的一个竖直平面内的平面运动，它可以用两个直线运动描述。本问题讨论的是子弹在通过抛射点的不同竖直平面内的运动，必须在三维空间中加以讨论。但是，每次抛射，子弹仍在一个平面内适动。
任意取一个过O点的竖直抛射平面，其与地面交线取作
轴，它与墙面交于点D，
，如图乙所示。若墙上瞄准点为B，子弹击中墙平面上直线MN上的A点。设B点坐标为
，因墙平面上各点的x坐标均为d。题中要求写出满足条件的y与x之间的函数关系。
我们把子弹的抛体运动分解为以速度为
的匀速直线运动和沿竖直方向的自由落体运动，且子弹击中直线MN上的A点。利用子弹匀速地从O点到B点的时间等于从B点自由落体到A点的时间，写出方程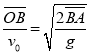
，
即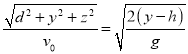
。
将此式两边平方，再整理得到
。
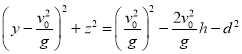这就是为击中墙上水平线MN，要求枪在墙上的瞄准点所满足的关系。这是一个圆方程，圆心坐标为
，圆半径为
。
图丙中画出了墙平面上的直线MN和瞄准点构成的圆。
能够看出：
ⅰ.一般情况下，同一个击中点A，对应有两个瞒准点
和
，即对应两个抛射角。因此，为使墙上击中点高于直线MN，在初速相同的情况下，其瞄准点应落在圆的内部。
ⅱ.当子弹初速、墙与发射点距离d、墙平面上直线MN高度h一定时，子弹只能击中此水平线的一部分，即从点
到点
一段。
ⅲ.瞄准点圆半径必须满足
。相应地，不能太小。代入r的表达式，确定的条件为
。
