Question

【题目】已知AB是圆O的切线，圆的半径为2， ，延长BO到C使得BC=6，BC与圆的另一个交点为E．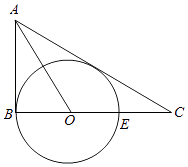

（Ⅰ）证明：AC是圆O的切线；
（Ⅱ）设AC与圆O的切点为F，求证：EF∥AO．

Answer 1

【答案】证明：（Ⅰ）∵ ，

∴ ，

点B到直线AC的距离为 ，

又 ，∴点O到直线AC的距离为点B到直线AC距离的 ，

即 ，即点O到直线AC的距离等于圆的半径，

∴AC是圆O的切线．…

（Ⅱ）如图， ，∴∠C=30°，

在△COF中，∠CFO=90°，∴∠COF=60°，

∴△OEF是等边三角形，∴∠OEF=60°．∠BOF=120°，

又△ABO≌△AFO，∴ ，

即∠AOB=∠OEF，∴EF∥AO．…

【解析】（1）根据勾股定理求出AC的值，再求出点B到直线AC的距离，根据比例关系可得到点O到直线AC的距离为点B到直线AC距离的,由此能证明 AC是圆O的切线，（2）根据正弦值可得∠C=30°，即∠COF=60°，不难推出△OEF是等边三角形，进而得到∠OEF=60°．∠BOF=120°，根据全等可得到∠ A O B = ∠ B O D = 60 °，即∠AOB=∠OEF，则EF∥AO．