Question

【题目】在平面直角坐标系 xy 中，椭圆E: （a>b>0）的离心率为 焦距为2.
( 14分)
（Ⅰ）求椭圆E的方程。
（Ⅱ）如图，该直线l：y=k1x- 交椭圆K于A,B两点，C是椭圆上的一点，直线OC的斜率为l1,且看k1l1= ,M是线段OC延长线上的一点，且|MC|:|AB|=2:3, ⊙M的半径为|MC|，OS:OT是⊙M的两条切线，切点分别为S.T，求∠SOT的最大值并求取得最大值时直线l的斜率。

Answer 1

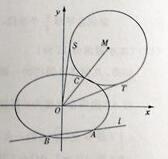
【答案】解：（I）由题意知 ， ， 所以 ，
因此 椭圆 的方程为 .
（Ⅱ）设 ，
联立方程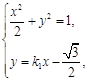
得 ，
由题意知 ，
且 ，
所以 .
由题意知 ，
所以
由此直线 的方程为 .
联立方程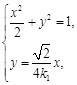
得 ，
因此 .
由题意可知 ，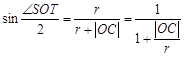
而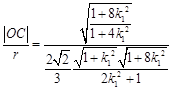
，
令 ，
则 ，
因此 ，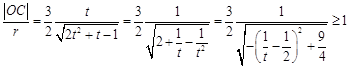
当且仅当 ，即 时等号成立，此时 ，
所以 ，
因此 ，
所以 最大值为 .
综上所述： 的最大值为 ，取得最大值时直线 的斜率为 .
【解析】正在更新中