题目内容
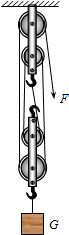
用如图所示的滑轮组提起重物（不计绳子重量和摩擦）．（1）当物重为180N时，滑轮组的机械效率为60%，则绳子末端拉力为
（2）该滑轮组中动滑轮的总重为
（3）当被提重物为240N重物上升3m时，则绳子末端拉力所做的功为
分析：（1）已知物体的重力和机械效率以及动滑轮上绳子的段数，根据公式η=
可求绳子的拉力．
（2）根据公式η=
可求动滑轮的总重．
（3）已知动滑轮上绳子的段数和物体升高的高度，可求绳子末端移动的距离，已知物体的重力和动滑轮的重力，可求拉力的大小，根据公式W=FS可求绳子末端拉力所做的功．
| W有用 |
| W总 |
（2）根据公式η=
| G |
| G+G动 |
（3）已知动滑轮上绳子的段数和物体升高的高度，可求绳子末端移动的距离，已知物体的重力和动滑轮的重力，可求拉力的大小，根据公式W=FS可求绳子末端拉力所做的功．
解答：解：（1）动滑轮上有3段绳子，
机械效率η=
=
=
；
所以绳子末端拉力为F=
=
=100N．
（2）不计绳子重量和摩擦，绳子末端拉力F=
，
所以动滑轮的总重G动=3F-G=3×100N-180N=120N．
（3）绳子末端移动的距离S1=3h1=3×3m=9m；
拉力F1=
=
=120N；
所以绳子末端拉力所做的功为W=F1S1=120N×9m=1080J．
故答案为：100；120；1080．
机械效率η=
| W有用 |
| W总 |
| Gh |
| FS |
| G |
| 3F |
所以绳子末端拉力为F=
| G |
| 3η |
| 180N |
| 3×60% |
（2）不计绳子重量和摩擦，绳子末端拉力F=
| G+G动 |
| 3 |
所以动滑轮的总重G动=3F-G=3×100N-180N=120N．
（3）绳子末端移动的距离S1=3h1=3×3m=9m；
拉力F1=
| G1+G动 |
| 3 |
| 240N+120N |
| 3 |
所以绳子末端拉力所做的功为W=F1S1=120N×9m=1080J．
故答案为：100；120；1080．
点评：本题考查拉力、动滑轮重力、做功的计算，关键是公式及其变形的灵活运用，重点是判断出动滑轮上绳子的段数．
练习册系列答案
相关题目
一个工人用如图所示的滑轮组提起重2000N的货物，所用的拉力是800N，绳子自由端被拉下4m，下列说法正确的是（ ）| A、总功是3200J，机械效率是40% | B、有用功是2000J，总功是3200J | C、有用功是3200J，机械效率是62.5% | D、总功是3200J，机械效率是62.5% |
用如图所示的滑轮组提起重1000N的货物，所用拉力是400N，绳的自由端被拉下2m．关于这个滑轮组工作的下列说法中，正确的是（ ）| A、总功是800J | B、额外功是100J | C、有用功是400J | D、机械效率是62.5% |
（2012?丹东模拟）用如图所示的滑轮组提起重300N的物体，如果不计动滑轮重、绳重和摩擦，则拉力F为
用如图所示的滑轮组提起重1000N的货物，所用拉力是400N，绳的自由端被拉下2m．关于这个滑轮组工作的下列说法中，正确的是（ ）
用如图所示的滑轮组提起重为900N的物体A，使物体在1min内上升了4m，所用的拉力为400N，