题目内容
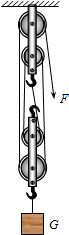
 用如图所示的滑轮组提升重物.已知物重为250N,动滑轮总重为30N,绳重及摩擦不计.
用如图所示的滑轮组提升重物.已知物重为250N,动滑轮总重为30N,绳重及摩擦不计.(1)给你一根能承受60N拉力的绳子,请在图中画出滑轮组的绕法;
(2)匀速提升重物时,绳端的拉力是多大?
(3)滑轮组的机械效率是多大?
(4)用这个滑轮组提升重物,它的机械效率最大为何值?
分析:(1)滑轮组绳子的绕法有两种:一是绳子先系在定滑轮的固定挂钩上,然后再绕过下面的动滑轮再向上绕到定滑轮上,依次反复绕,这种绕法有偶数段绳子承担物重;
二是绳子先系在动滑轮的固定挂钩上,然后再绕过上面的定滑轮再向下,依次反复绕,这种绕法有奇数段绳子承担物重.分别求出拉力大小和绳子能承受的最大拉力进行比较后选择.
(2)由(1)可知,承担物重的绳子股数n、物重、拉力F的大小,利用效率公式计算滑轮组的机械效率;
(3)用同一个滑轮组提升重物,提升的重物越重,机械效率越高;知道绳子能承受的最大拉力,求出F=
(G物+G轮)能提升的最大物重,再利用效率公式求滑轮组的最大机械效率.
二是绳子先系在动滑轮的固定挂钩上,然后再绕过上面的定滑轮再向下,依次反复绕,这种绕法有奇数段绳子承担物重.分别求出拉力大小和绳子能承受的最大拉力进行比较后选择.
(2)由(1)可知,承担物重的绳子股数n、物重、拉力F的大小,利用效率公式计算滑轮组的机械效率;
(3)用同一个滑轮组提升重物,提升的重物越重,机械效率越高;知道绳子能承受的最大拉力,求出F=
| 1 |
| 5 |
解答: 解:(1)滑轮组绕线有两种,如右图:
解:(1)滑轮组绕线有两种,如右图:
因滑轮组的摩擦不计,动滑轮的重为30N,当使用甲图中滑轮组,绳子的股数是四股,则拉力:
F甲=
=
=70N>60N;
即拉力会大于绳子承受的最大拉力60N,故不能选择;
当使用乙图中滑轮组,绳子的股数是五股,拉力:
F乙=
=
=56N<60N,
拉力小于绳子承受的最大力,故选择乙图.
(2)由(1)可知,n=5,s=5h,F=56N,G=250N,
此时滑轮组的机械效率:
η=
=
=
≈89%;
(3)∵F=
(G物+G轮),绳子能承受的最大拉力为60N,
∴能提升的最大物重:
G大=5F大-G轮=5×60N-30N=270N,
此时滑轮组的机械效率:
η′=
=
=
=90%.
答:(1)滑轮组的绕法如乙图;
(2)匀速提升重物时,绳端的拉力是56N;
(3)滑轮组的机械效率是89%;
(4)用这个滑轮组提升重物,它的机械效率最大为90%.
 解:(1)滑轮组绕线有两种,如右图:
解:(1)滑轮组绕线有两种,如右图:因滑轮组的摩擦不计,动滑轮的重为30N,当使用甲图中滑轮组,绳子的股数是四股,则拉力:
F甲=
| G物+G动 |
| n甲 |
| 250N +30N |
| 4 |
即拉力会大于绳子承受的最大拉力60N,故不能选择;
当使用乙图中滑轮组,绳子的股数是五股,拉力:
F乙=
| G物+G动 |
| n乙 |
| 250N +30N |
| 5 |
拉力小于绳子承受的最大力,故选择乙图.
(2)由(1)可知,n=5,s=5h,F=56N,G=250N,
此时滑轮组的机械效率:
η=
| W有 |
| W总 |
| Gh |
| Fs |
| 250N×h |
| 56N×5h |
(3)∵F=
| 1 |
| 5 |
∴能提升的最大物重:
G大=5F大-G轮=5×60N-30N=270N,
此时滑轮组的机械效率:
η′=
| W′有 |
| W′总 |
| G大h |
| F大s |
| 270N×h |
| 60N×5h |
答:(1)滑轮组的绕法如乙图;
(2)匀速提升重物时,绳端的拉力是56N;
(3)滑轮组的机械效率是89%;
(4)用这个滑轮组提升重物,它的机械效率最大为90%.
点评:本题考查了滑轮组的绕法、机械效率的计算,在绳重及摩擦不计时,灵活运用公式F=
(G物+G轮)是本题的关键.
| 1 |
| n |

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 一个工人用如图所示的滑轮组提起重2000N的货物,所用的拉力是800N,绳子自由端被拉下4m,下列说法正确的是( )
一个工人用如图所示的滑轮组提起重2000N的货物,所用的拉力是800N,绳子自由端被拉下4m,下列说法正确的是( )| A、总功是3200J,机械效率是40% | B、有用功是2000J,总功是3200J | C、有用功是3200J,机械效率是62.5% | D、总功是3200J,机械效率是62.5% |
 用如图所示的滑轮组提起重1000N的货物,所用拉力是400N,绳的自由端被拉下2m.关于这个滑轮组工作的下列说法中,正确的是( )
用如图所示的滑轮组提起重1000N的货物,所用拉力是400N,绳的自由端被拉下2m.关于这个滑轮组工作的下列说法中,正确的是( )| A、总功是800J | B、额外功是100J | C、有用功是400J | D、机械效率是62.5% |
 (2012?丹东模拟)用如图所示的滑轮组提起重300N的物体,如果不计动滑轮重、绳重和摩擦,则拉力F为
(2012?丹东模拟)用如图所示的滑轮组提起重300N的物体,如果不计动滑轮重、绳重和摩擦,则拉力F为 用如图所示的滑轮组提起重1000N的货物,所用拉力是400N,绳的自由端被拉下2m.关于这个滑轮组工作的下列说法中,正确的是( )
用如图所示的滑轮组提起重1000N的货物,所用拉力是400N,绳的自由端被拉下2m.关于这个滑轮组工作的下列说法中,正确的是( ) 用如图所示的滑轮组提起重为900N的物体A,使物体在1min内上升了4m,所用的拉力为400N,
用如图所示的滑轮组提起重为900N的物体A,使物体在1min内上升了4m,所用的拉力为400N,