题目内容
汽车匀速行驶,在距离隧道右侧入口165m处开始鸣笛,司机经过1s听到回声,此时,他看到这条长200m的隧道内有一工人正在检修设备,立即亮灯提醒工人离开.恰好工人正好处在向左、向右跑都能安全脱险的位置.当时声音的速度v声=315m/s.问:(1)工人所处位置距右出口的距离是多少?
(2)他奔跑的最小速度是多大?
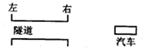
【答案】分析:笛声传播的同时汽车也在行驶,笛声传播的路程和汽车行驶的路程的总和等于鸣笛处到隧道口距离的2倍,鸣笛处到隧道口距离为165mm,则笛声传播的路程和汽车行驶的路程的总和等于330mm,已知笛声的速度、时间和总路程,根据速度公式求出汽车的行驶速度.求出汽车到左右隧道口的路程,利用速度公式求汽车到左右隧道口用的时间;
设工人距右出口的距离为s右,则距离左出口的距离为200m-s右,设最小奔跑速度为v,则得出方程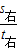 =
= ,解得s右和v,即工人所处位置距右出口的距离和他奔跑的最小速度.
,解得s右和v,即工人所处位置距右出口的距离和他奔跑的最小速度.
解答:解:
笛声传播的路程和汽车行驶的路程的总和:s总=165m×2=330m,
笛声传播的路程s声=v声t=315m/s×1s=315m,
汽车行驶的路程s车=s总-s声=330m-315m=15m,
汽车的速度为:v车=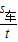 =
=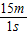 =15m/s,
=15m/s,
汽车到隧道右出口的距离:
s=165m,
∵v= ,
,
∴汽车到达隧道右出口的时间:
t右=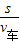 =
=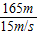 =11s,
=11s,
汽车到达隧道左出口的时间:
t左=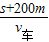 =
=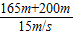 ≈24.3s,
≈24.3s,
设工人距右出口的距离为s右,则距离左出口的距离为200m-s右,设最小奔跑速度为v,则
向右跑时:v=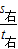 ,
,
向左跑时:v=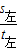 =
= ,
,
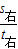 =
= ,
,
即: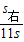 =
=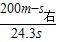 ,
,
解得:s右≈62.3m,
最小奔跑速度:
v=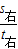 =
=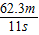 ≈5.7m/s.
≈5.7m/s.
答:(1)工人所处位置距右出口的距离是62.3m;
(2)他奔跑的最小速度是5.7m/s.
点评:本题考查了学生对速度公式的掌握和运用,根据汽车的行驶路程和速度,求出左右隧道口的时间,即工人跑到左右隧道口的时间是本题的关键,难点所在!
设工人距右出口的距离为s右,则距离左出口的距离为200m-s右,设最小奔跑速度为v,则得出方程
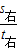 =
= ,解得s右和v,即工人所处位置距右出口的距离和他奔跑的最小速度.
,解得s右和v,即工人所处位置距右出口的距离和他奔跑的最小速度.解答:解:
笛声传播的路程和汽车行驶的路程的总和:s总=165m×2=330m,
笛声传播的路程s声=v声t=315m/s×1s=315m,
汽车行驶的路程s车=s总-s声=330m-315m=15m,
汽车的速度为:v车=
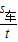 =
=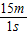 =15m/s,
=15m/s,汽车到隧道右出口的距离:
s=165m,
∵v=
 ,
,∴汽车到达隧道右出口的时间:
t右=
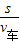 =
=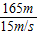 =11s,
=11s,汽车到达隧道左出口的时间:
t左=
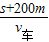 =
=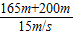 ≈24.3s,
≈24.3s,设工人距右出口的距离为s右,则距离左出口的距离为200m-s右,设最小奔跑速度为v,则
向右跑时:v=
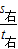 ,
,向左跑时:v=
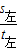 =
= ,
,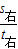 =
= ,
,即:
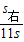 =
=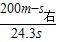 ,
,解得:s右≈62.3m,
最小奔跑速度:
v=
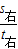 =
=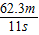 ≈5.7m/s.
≈5.7m/s.答:(1)工人所处位置距右出口的距离是62.3m;
(2)他奔跑的最小速度是5.7m/s.
点评:本题考查了学生对速度公式的掌握和运用,根据汽车的行驶路程和速度,求出左右隧道口的时间,即工人跑到左右隧道口的时间是本题的关键,难点所在!

练习册系列答案
相关题目
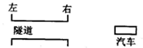 汽车匀速行驶,在距离隧道右侧入口165m处开始鸣笛,司机经过1s听到回声,此时,他看到这条长200m的隧道内有一工人正在检修设备,立即亮灯提醒工人离开.恰好工人正好处在向左、向右跑都能安全脱险的位置.当时声音的速度v声=315m/s.问:
汽车匀速行驶,在距离隧道右侧入口165m处开始鸣笛,司机经过1s听到回声,此时,他看到这条长200m的隧道内有一工人正在检修设备,立即亮灯提醒工人离开.恰好工人正好处在向左、向右跑都能安全脱险的位置.当时声音的速度v声=315m/s.问: