题目内容
 如图所示,一根细绳悬挂一个半径为r米、质量为m千克的半球,半球的底面与容器底部紧密接触,此容器内液体的密度为ρ千克/米3,高度为H米,大气压强为p0帕,已知球体的体积公式是V=4πr3/3,球面积公式是S球=4πr2,圆面积公式是S圆=πr2.则液体对半球的压力为
如图所示,一根细绳悬挂一个半径为r米、质量为m千克的半球,半球的底面与容器底部紧密接触,此容器内液体的密度为ρ千克/米3,高度为H米,大气压强为p0帕,已知球体的体积公式是V=4πr3/3,球面积公式是S球=4πr2,圆面积公式是S圆=πr2.则液体对半球的压力为πr2ρgH-
ρgπr3
| 2 |
| 3 |
πr2ρgH-
ρgπr3
牛.若要把半球从水中拉起,则至少要用| 2 |
| 3 |
πr2ρgH-
ρgπr3+mg+p0πr2
| 2 |
| 3 |
πr2ρgH-
ρgπr3+mg+p0πr2
牛的竖直向上的拉力.| 2 |
| 3 |
分析:浸没在液体中的固态受到的浮力等于固态各表面所受液体压力的合力;我们可以先设想半球体下表面有液体,求出此时下表面受到的液体压力和半球体受到的浮力,从而求出此时液体对半球体上表面的压力;然后对半球体进行受力分析,求出把半球体从水中拉起需要的拉力.
解答: 解:(1)假设半球下表面处全部为液体,
解:(1)假设半球下表面处全部为液体,
则半球受到的浮力F浮方向竖直向上,由阿基米德原理可知,
F浮=ρgV排=ρgV半球=ρg×
×
πr3=
ρgπr3;
半球表面各处所受液体压力的分布如图所示,
半球上表面受到的液体压力F上竖直向下,
∵P=
,∴F=PS,半球下表面受到的液体压力:
F下=P下S圆=P液S圆=ρgH×πr2,方向竖直向上,
半球受到的浮力F浮等于半球下表面与上表面所受液体对它的压力合力,
即:F浮=F下-F上,F上=F下-F浮=πr2ρgH-
ρgπr3,
在本题给出的条件中,半球底部与容器底部紧密接触,即半球的下表面处并不与液体接触,
但这并不改变半球上表面受液体压力作用的情况,则液体对半球的压力仍为F上=πr2ρgH-
ρgπr3;
(2)半球刚要被拉起时,容器底板对半球的下表面已无向上的支持力,
则竖直向上的拉力F拉至少要等于上述的F上与半球本身的重力之和,
即:F拉=F上+mg=πr2ρgH-
ρgπr3+mg+p0πr2.
故答案为:πr2ρgH-
ρgπr3;πr2ρgH-
ρgπr3+mg+p0πr2.
 解:(1)假设半球下表面处全部为液体,
解:(1)假设半球下表面处全部为液体,则半球受到的浮力F浮方向竖直向上,由阿基米德原理可知,
F浮=ρgV排=ρgV半球=ρg×
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
半球表面各处所受液体压力的分布如图所示,
半球上表面受到的液体压力F上竖直向下,
∵P=
| F |
| S |
F下=P下S圆=P液S圆=ρgH×πr2,方向竖直向上,
半球受到的浮力F浮等于半球下表面与上表面所受液体对它的压力合力,
即:F浮=F下-F上,F上=F下-F浮=πr2ρgH-
| 2 |
| 3 |
在本题给出的条件中,半球底部与容器底部紧密接触,即半球的下表面处并不与液体接触,
但这并不改变半球上表面受液体压力作用的情况,则液体对半球的压力仍为F上=πr2ρgH-
| 2 |
| 3 |
(2)半球刚要被拉起时,容器底板对半球的下表面已无向上的支持力,
则竖直向上的拉力F拉至少要等于上述的F上与半球本身的重力之和,
即:F拉=F上+mg=πr2ρgH-
| 2 |
| 3 |
故答案为:πr2ρgH-
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题难度较大,是一道难题,知道浮力产生的原因、熟练应用压强公式的变形公式、液体压强公式、对半球正确受力分析等是正确解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目


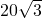 牛
牛 牛
牛 牛
牛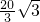 牛
牛


