题目内容
19.如图所示,均匀棒AB可绕A点转动,平衡时恰有一半浸入水中,求棒的密度.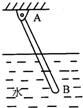
分析 A为杠杆的支点,O为重力G的作用点,也正好是杠杆长度的一半;因此杠杆均匀,且有一半浸在水中,则浮力的作用点在点P处,也正好是OB的中间位置.作出两个力的力臂,根据三角形的关系和杠杆的平衡条件可求得棒的密度.
解答 解:如图所示,A为杠杆的支点,O为重力G的作用点,AC为重力的力臂,AD为浮力的力臂,△AOC∽△APD,
则$\frac{AO}{AP}$=$\frac{AC}{AD}$=$\frac{2}{3}$.
由杠杆的平衡条件得,2G=3F浮
则2ρ木gV木=3ρ水gV排,V排=$\frac{1}{2}$V木,
解得ρ木=$\frac{3}{4}$ρ水=0.75×103kg/m3.
答:棒的密度为0.75×103kg/m3.
点评 此题考查密度的计算,涉及到浮力的计算,杠杆的平衡条件的应用,相似三角形的性质等,解答此题要求学生应具备一定的学科综合能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
7.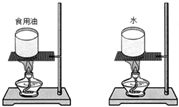 为了比较水和食用油的某种特性,小明用两个相同的装置做了如图所示的实验.用温度计测量液体吸收热量后升高的温度值,并用钟表记录加热时间.实验数据记录如表.
为了比较水和食用油的某种特性,小明用两个相同的装置做了如图所示的实验.用温度计测量液体吸收热量后升高的温度值,并用钟表记录加热时间.实验数据记录如表.
(1)在实验过程中控制加热时间相同,是为了使两种液体吸收的热量相等,通过比较升高的温度来研究水和食用油吸热能力的差异.
(2)在此实验中,如果要使水和食用油的最后温度相同,就要给水加热更长的时间,此时水吸收的热量大于(选填“大于”或“小于”或“等于”)食用油吸收的热量.
(3)通过实验可以得到不同的物质吸热能力不同,物质的这种特性用比热容这个物理量来描述.
 为了比较水和食用油的某种特性,小明用两个相同的装置做了如图所示的实验.用温度计测量液体吸收热量后升高的温度值,并用钟表记录加热时间.实验数据记录如表.
为了比较水和食用油的某种特性,小明用两个相同的装置做了如图所示的实验.用温度计测量液体吸收热量后升高的温度值,并用钟表记录加热时间.实验数据记录如表.| 物质 | 质量/g | 初始温度/℃ | 加热时间/min | 最后温度/℃ |
| 水 | 60 | 20 | 6 | 45 |
| 食用油 | 60 | 20 | 6 | 68 |
(2)在此实验中,如果要使水和食用油的最后温度相同,就要给水加热更长的时间,此时水吸收的热量大于(选填“大于”或“小于”或“等于”)食用油吸收的热量.
(3)通过实验可以得到不同的物质吸热能力不同,物质的这种特性用比热容这个物理量来描述.