题目内容
 如图所示,底面积为Sb的圆柱形容器内盛有适量的水,另一底面积为Sa的圆柱体A有部分体积浸在水中,当圆柱体A相对于容器下降高度为h时(水没有溢出,圆柱体A也未全部没入水中),以下说法中正确的是
如图所示,底面积为Sb的圆柱形容器内盛有适量的水,另一底面积为Sa的圆柱体A有部分体积浸在水中,当圆柱体A相对于容器下降高度为h时(水没有溢出,圆柱体A也未全部没入水中),以下说法中正确的是
- A.容器中水面升高了

- B.容器中的水面升高了

- C.圆柱体A所受水的浮力增加了

- D.容器底所受到的水的压力增加了ρ水gSah
BC
分析:(1)设圆柱体A原来排开水的体积为V排,圆柱体下降h后排开水的体积为 V排′,则V排=Sah′、V排′=Sah′+Sa(h+△h),据此求出A排开水的体积的变化,而△V排=Sb△h,求出容器中水面升高值;
(2)求出容器中水面升高值,可求排开水的体积变化值,再利用阿基米德原理求圆柱体A所受水的浮力增加值;
(3)求出容器中水面升高值,利用液体压强公式求容器底所受到的水的压强增加值,再利用F=pS求容器底所受到的水的压力增加值.
解答: 解:
解:
AB、圆柱体A原来排开水的体积为V排,则V排=Sah′,
圆柱体下降h后排开水的体积为 V排′,则V排′=Sah′+Sa(h+△h)
排开水的体积的变化:
△V排=V排′-V排=Sah′+Sa(h+△h)-Sah′=Sa(h+△h),
而△V排=Sb△h,
∴Sa(h+△h)=Sb△h,
解得:
△h= h,故A错、B正确;
h,故A错、B正确;
C、△V排=Sb?△h= h,
h,
△F浮=ρ水g△V排=ρ水g h,故C正确;
h,故C正确;
D、容器底所受到的水的压强增加了:
△p=ρ水g△h=ρ水g h,
h,
∵p=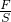 ,
,
∴容器底所受到的水的压力增加了:
△F=△pS=ρ水g△hSb=ρ水g h,故D错.
h,故D错.
故选BC.
点评:本题为力学综合题,考查了学生对液体压强公式、压强定义式、阿基米德原理的理解和应用,关键是对物体排开液体体积的判断,是本题的一个难点.
分析:(1)设圆柱体A原来排开水的体积为V排,圆柱体下降h后排开水的体积为 V排′,则V排=Sah′、V排′=Sah′+Sa(h+△h),据此求出A排开水的体积的变化,而△V排=Sb△h,求出容器中水面升高值;
(2)求出容器中水面升高值,可求排开水的体积变化值,再利用阿基米德原理求圆柱体A所受水的浮力增加值;
(3)求出容器中水面升高值,利用液体压强公式求容器底所受到的水的压强增加值,再利用F=pS求容器底所受到的水的压力增加值.
解答:
 解:
解:AB、圆柱体A原来排开水的体积为V排,则V排=Sah′,
圆柱体下降h后排开水的体积为 V排′,则V排′=Sah′+Sa(h+△h)
排开水的体积的变化:
△V排=V排′-V排=Sah′+Sa(h+△h)-Sah′=Sa(h+△h),
而△V排=Sb△h,
∴Sa(h+△h)=Sb△h,
解得:
△h=
 h,故A错、B正确;
h,故A错、B正确;C、△V排=Sb?△h=
 h,
h,△F浮=ρ水g△V排=ρ水g
 h,故C正确;
h,故C正确;D、容器底所受到的水的压强增加了:
△p=ρ水g△h=ρ水g
 h,
h,∵p=
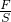 ,
,∴容器底所受到的水的压力增加了:
△F=△pS=ρ水g△hSb=ρ水g
 h,故D错.
h,故D错.故选BC.
点评:本题为力学综合题,考查了学生对液体压强公式、压强定义式、阿基米德原理的理解和应用,关键是对物体排开液体体积的判断,是本题的一个难点.

练习册系列答案
相关题目
 (2013?呼和浩特)如图所示,底面积为S的圆筒形容器,高h,装有体积是V的水,水底有一静止的边长为L的正方体实心铝块,密度为ρ1,水的密度ρ水.已知g.求:
(2013?呼和浩特)如图所示,底面积为S的圆筒形容器,高h,装有体积是V的水,水底有一静止的边长为L的正方体实心铝块,密度为ρ1,水的密度ρ水.已知g.求: 如图所示,底面积为S的薄壁玻璃杯放在水平桌面上,其中盛有重为G1的水,将一块重为G2、边长为d的正立方体木块放入水中漂浮,杯中水未溢出,水面升高了h.下列说法错误的是( )
如图所示,底面积为S的薄壁玻璃杯放在水平桌面上,其中盛有重为G1的水,将一块重为G2、边长为d的正立方体木块放入水中漂浮,杯中水未溢出,水面升高了h.下列说法错误的是( ) 如图所示,底面积为S的圆筒形容器,高h,装有体积是V的水,水底有一静止的边长为L的正方体实心铝块,密度为ρ1,水的密度ρ水.已知g.求:
如图所示,底面积为S的圆筒形容器,高h,装有体积是V的水,水底有一静止的边长为L的正方体实心铝块,密度为ρ1,水的密度ρ水.已知g.求:


