题目内容
甲乙两立方体的边长之比是2:1,质量之比是4:3,则甲乙两物体的密度之比是________.某一物体做变速直线运动,已知它在前一半路程的速度位4m/s,后一半路程的速度是6m/s,那么,它在整个路程中的平均速度是________.
1:6 4.8m/s
分析:①已知立方体边长之比可以得到体积;已知质量之比和体积之比,利用公式ρ= 得到密度之比;
得到密度之比;
②由速度的变形公式求出物体在前一半与后一般路程的运动时间,然后应用速度公式求出整个过程的平均速度.
解答:
①已知立方体边长之比为2:1,所以体积之比为V1:V2=8:1,
∵ρ= ,∴
,∴ =
= =
=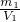 ×
× =
= ×
× =
= ;
;
②设整个过程的路程是2s,则前半段与后半段路程都是s,
∵v= ,
,
∴物体的运动时间:
t1=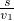 =
= ,
,
t2=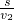 =
= ,
,
总的运动时间t=t1+t2,
整个过程的平均速度:
v=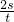 =
= =
= =4.8m/s.
=4.8m/s.
故答案为:1:6;4.8m/s.
点评:①比值的计算是物理中常见的题型,解题时的方法是,明确需求量和已知量之间的关系,找出相应的关系式,然后条理清楚地进行运算,切不可想象心算.
②平均速度不等于速度的平均,全程的平均速度等于总路程除以总时间.
分析:①已知立方体边长之比可以得到体积;已知质量之比和体积之比,利用公式ρ=
 得到密度之比;
得到密度之比;②由速度的变形公式求出物体在前一半与后一般路程的运动时间,然后应用速度公式求出整个过程的平均速度.
解答:
①已知立方体边长之比为2:1,所以体积之比为V1:V2=8:1,
∵ρ=
 ,∴
,∴ =
= =
=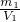 ×
× =
= ×
× =
= ;
;②设整个过程的路程是2s,则前半段与后半段路程都是s,
∵v=
 ,
,∴物体的运动时间:
t1=
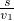 =
= ,
,t2=
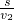 =
= ,
,总的运动时间t=t1+t2,
整个过程的平均速度:
v=
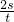 =
= =
= =4.8m/s.
=4.8m/s.故答案为:1:6;4.8m/s.
点评:①比值的计算是物理中常见的题型,解题时的方法是,明确需求量和已知量之间的关系,找出相应的关系式,然后条理清楚地进行运算,切不可想象心算.
②平均速度不等于速度的平均,全程的平均速度等于总路程除以总时间.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
甲、乙两立方体的边长之比是2:1,质量之比是4:3,那么甲、乙两物体的密度之比是( )
| A、3:8 | B、4:6 | C、1:6 | D、2:3 |