题目内容
甲、乙两个作匀速直线运动的物体从同一地点出发,向同一方向运动,甲的速度为2米/秒,乙的速度为6米/秒。当甲运动20秒后乙开始运动,用图解法求出甲、乙两物体相遇的时间和路程。
【分析】若用图解法求此题,有两种解法。一是利用速度一时间图像;二是利用路程一时间图像。
【解法一】利用速度--时间图像。如图2-4所示。线AB是甲的速度图线,线CD是乙的速度图线,根据速度-时间图像的特点,矩形ABNO的面积表示甲物体通过的路程,矩形CDNM的面积表示乙物体通过的路程。甲、乙相遇时通过的路程相等。即SABNO=SCDNM又SPBNM为公共区域。
故只需SAPMO=SCDBP即可即OA×OM=CP×PB
根据已知条件:OA=2米/秒
OM=20秒 CP=CM-CP=6米/秒-2米/秒=4米/秒
将已知条件代入上式得 PB=10秒
即MN=10秒ON=30秒
当甲物体运动30秒,乙物体运动10秒后,两物体相遇。可算出此时离出发点距离为60米。
【解法二】利用路程时间图像。
如图2-5所示,甲运动20秒后乙才开始运动。所以,乙图线的起始点应从时间轴上20秒处画起,两图线倾斜度不同,表示物体运动速度不同。两条图线相交于P点,从P点作时间轴的垂线交于A,可知甲物体运动30秒,乙物体运动10秒后相遇。从P点作一条路程轴的垂线交于B,可知,甲、乙两物体通过了60米的路程。相遇时二人离他们的出发点60米。
【评注】利用图像法解题是一种方法,有些时候,用图像法是比较直观,比较简便的方法。

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案小华的物理老师在上课之前,测定了额定电压为2.5V小灯泡的I与U的关系的数据如下表所示:
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
U/V | 0.20 | 0.80 | 1.40 | 2.00 | 2.50 | 2.90 |
I/A | 0.02 | 0.08 | 0.14 | 0.18 | 0.20 | 0.21 |
(1)从数据可知,该小灯泡的额定电流为______A,正常发光时的电阻为______Ω,额定功率为______W。
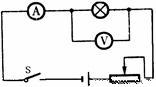
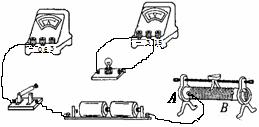
(2)小华想亲自做一次,看能否测得同样的数据。于是她设计了如题(a)图所示的电路,准备对该小灯泡进行再次测量,小华找来了实验器材并连接了部分实物电路,其中电源用的是2节干电池,滑动变阻器的铭牌标有“50Ω1A”。
①请你用笔画线代替导线,按照题(a)图所示电路,帮小华将题(b)图中缺少的两根导线补充连接完整。
(a) (b)
②闭合开关前,滑动变阻器的滑片应移到______端(选填“A”或“B”);闭合开关后,发现灯泡不亮,电流表无示数,但电压表有示数,则电路可能出现的故障是______。
③小华能通过这个实验得到上述表格中的每一组实验数据吗?______(填“能”或“不能”),理由是______。