题目内容
17. 一质量为6kg的石块,沉在装水的容器底部,某同学用一动滑轮将石块从水中匀速提起1m,但石块没有露出水面,如图所示,已知绳的自由端拉力为25N.求石块在上升过程中:(ρ石=3×103kg/m3、g=10N/kg )
一质量为6kg的石块,沉在装水的容器底部,某同学用一动滑轮将石块从水中匀速提起1m,但石块没有露出水面,如图所示,已知绳的自由端拉力为25N.求石块在上升过程中:(ρ石=3×103kg/m3、g=10N/kg )(1)石块受到的浮力为多少?
(2)绳的自由端拉力做功为多少?
(3)动滑轮的机械效率为多少?
(4)石块底面的压强变化多少?
分析 (1)知道石块的质量和密度,利用密度公式求石块的体积,因为石块浸没在水中,所以排开水的体积等于石块体积,再利用阿基米德原理F浮=ρ水gV排求出石块受到的浮力;
(2)图中使用的是动滑轮,则s=2h,求出拉力移动的距离,又知道拉力大小,利用W=Fs求绳的自由端拉力做功;
(3)知道石块的质量,利用重力公式求石块的重,此时石块重等于石块受到的浮力加上动滑轮对石块的拉力,据此求出动滑轮对石块的拉力,可求利用动滑轮做的有用功,再利用效率公式求动滑轮的机械效率.
(4)求出石块底面深度的变化量,利用液体压强公式计算石块底面的压强变化量.
解答 解:(1)根据ρ=$\frac{m}{V}$可得,石块的体积:
V=$\frac{m}{{ρ}_{石}}$=$\frac{6kg}{3×1{0}^{3}kg/{m}^{3}}$=2×10-3m3,
石块浸没水中,则V排=V=2×10-3m3,
石块受到的浮力:F浮=ρ水gV排=1×103kg/m3×10N/kg×2×10-3m3=20N;
(2)由图知,绳子自由端移动的距离:s=2h=2×1m=2m,
绳的自由端拉力做功:W总=Fs=25N×2m=50J;
(3)石块重:G=mg=6kg×10N/kg=60N,
石块受向下的重力、向上的拉力和浮力而匀速运动,所以G=F拉+F浮,
则动滑轮对石块的拉力:F拉=G-F浮=60N-20N=40N,
利用动滑轮做的有用功:W有=F拉h=40N×1m=40J,
动滑轮的机械效率:
η=$\frac{{W}_{有}}{{W}_{总}}$×100%=$\frac{40J}{50J}$×100%=80%.
(4)石块底面受到水的压强变化量:
△p=p1-p2=ρ水gh1-ρ水gh2=ρ水g(h1-h2)=1×103kg/m3×10N/kg×1m=1×104pa.
答:(1)石块受到的浮力为20N;
(2)绳的自由端拉力做功为50J;
(3)动滑轮的机械效率为80%;
(4)石块底面的压强变化了1×104pa.
点评 本题考查了密度公式的应用、浮力的计算、有用功、总功、机械效率、液体压强的计算,涉及到的知识点较多,综合性强,属于难题.


| A. | 图甲所示,过山车向下运动时是重力势能转化为动能 | |
| B. | 图乙所示,水电站将水的机械能转化为电能 | |
| C. | 图丙所示,自行车运动员奋力蹬车时,人体内的一部分化学能转化为动能 | |
| D. | 图丁所示,汽车在刹车过程中,刹车片会发热,将内能转化为动能 |
| A. | ①和② | B. | ②和③ | C. | ①和④ | D. | ②和④ |
演绎式探究--原子内部电子绕原子核的运动
| (1)我们知道,原子有原子核和核外电子组成,核外电子绕原子核高速旋转.按照波尔理论,电子绕原子核做匀速圆周运动,且电子会受到原子核的静电吸引力(如图甲).已知,电子受到的静电吸引力F电与原子序数Z成正比,与元电荷e的平方成正比,与电子运动的轨道半径r的平方的关系如右图乙图象所示,k是静电常数.则电子所受的静电吸引力的数学表达式为:B. A.${F_电}=\frac{{Z{e^2}{r^2}}}{4πk}$B.${F_电}=\frac{{Z{e^2}}}{{4πk{r^2}}}$C.${F_电}=\frac{e^2}{{4πkZ{r^2}}}$D.${F_电}=\frac{{Z{r^2}}}{{4πk{e^2}}}$ 其中静电常数k=8.85×10-12,当物体做匀速圆周运动时,必须受到一个向圆心拉的力,这个力叫做向心力,电子绕原子核做匀速圆周运动的向心力${F_心}=m\frac{υ^2}{r}$,其中m为电子的质量,υ为电子的运动速度.且电子做圆周运动的向心力等于电子受到的静电吸引力. (2)波尔引用量子理论,提出电子运动的轨道不是任意的,轨道数n从内向外依次为1、2、3、…,(如图丙)并且提出$mυr=n\frac{h}{2π}$,其中n为轨道数,h为常数,h=6.63×10-34J•s.请推导出电子的轨道速度υ的数学表达式. (3)已知氧原子的原子序数Z=8,元电荷e=1.6×10-19C,求氧原子中电子在轨道数n=2的轨道上运动式的速度υ2= 8.73×106m/s. | 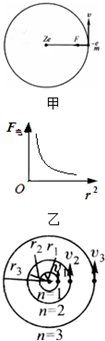 |

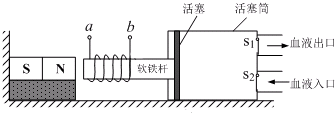
(1)根据实验数据计算出的大气压强为9×104Pa.
(2)为判断实验结果的准确性,小明利用自家汽车里的“胎压计”测量实际的大气压,示数如图乙所示,其值为1×105Pa.
(3)对比两次实验结果,小明认为实验中存在下列原因,其中一定不可能的是B.
A.注射器中有空气未全部排尽
B.活塞与注射器筒壁间摩擦较大
(4)小明还发现:如果在针筒内吸入一定质量的空气,然后用橡皮帽将气体封闭起来,在推活塞的过程中,越推越费力.由此小明猜想:其他条件一定时,封闭气体的体积越小,压强越大.
(5)为了验证自己的猜想,小明用一个30mL的注射器吸入一定质量的空气后连接到胎压计上,通过推拉活塞,测得数据记录如表:
| V/mL | 8 | 12 | 16 | 20 | 24 |
| p/kPa | 120 | 80 | 60 | 48 | 40 |
②当小明不推拉活塞时,注射器内的空气体积为9.6mL.
(6)你认为封闭气体的压强还可能与哪些因素有关,写出一个猜想以及你的依据.
①猜想:温度.②依据:夏天容易爆胎或压瘪的乒乓球放在热水中会复原.