题目内容
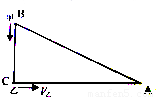
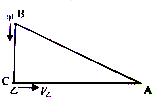 如图所示,B、C两点相距60米,C、A两点相距80米,AC与BC相互垂直.甲以2米/秒的速度由B点向C点运动,乙以4米/秒的速度同时由C点向A点运动.经过
如图所示,B、C两点相距60米,C、A两点相距80米,AC与BC相互垂直.甲以2米/秒的速度由B点向C点运动,乙以4米/秒的速度同时由C点向A点运动.经过6
6
秒,甲、乙之间的距离最近;经过| 90 |
| 11 |
| 90 |
| 11 |
分析:(1)甲从B向C运动到D点,乙从C向A运动E点,构成Rt△DCE,求出DC、CE,根据勾股定理求出DE,得到一个二次函数,当自变量为-
时二次函数有最小值.如图1.
(2)甲从B向C运动到D点,乙从C向A运动E点,△DCE∽△ACB,根据相似三角形对应线段成比例求出甲乙的运动时间.如图1.
甲从B向C运动到M点,乙从C向A运动N点,△CMN∽△CBA,根据相似三角形对应线段成比例求出甲乙的运动时间.如图2.

| b |
| 2a |
(2)甲从B向C运动到D点,乙从C向A运动E点,△DCE∽△ACB,根据相似三角形对应线段成比例求出甲乙的运动时间.如图1.
甲从B向C运动到M点,乙从C向A运动N点,△CMN∽△CBA,根据相似三角形对应线段成比例求出甲乙的运动时间.如图2.

解答:解:(1)设甲乙运动时间为t,
甲的运动速度为2m/s,乙的运动速度为4m/s,
根据速度公式得:DB=2m/s?t,CE=4m/s?t,
因为,BC=60m,所以DC=BC-BD=60m-2m/s?t,
根据勾股定理得,DE2=CD2+CE2,
设y=DE,所以,y2=(60m-2m/s?t)2+(4m/s?t)2,
整理得,y2=20t2-240t+3600,
当t=-
=-
=6s时,y最小,即甲乙距离最短.
(2)①如分析中图1:
甲从B向C运动到D点,乙从C向A运动E点,△DCE∽△ACB,
所以
=
,
=
.
t=
s.
②如分析中图2,甲从B向C运动到M点,乙从C向A运动N点,△CMN∽△CBA,
所以
=
,
CM=60m-2m/s?t,CN=4m/s?t,
=
,
所以,t=12s.
故答案为:6;
或12.
甲的运动速度为2m/s,乙的运动速度为4m/s,
根据速度公式得:DB=2m/s?t,CE=4m/s?t,
因为,BC=60m,所以DC=BC-BD=60m-2m/s?t,
根据勾股定理得,DE2=CD2+CE2,
设y=DE,所以,y2=(60m-2m/s?t)2+(4m/s?t)2,
整理得,y2=20t2-240t+3600,
当t=-
| b |
| 2a |
| -(-240) |
| 2×20 |
(2)①如分析中图1:
甲从B向C运动到D点,乙从C向A运动E点,△DCE∽△ACB,
所以
| DC |
| AC |
| CE |
| BC |
| 60m-2m/s?t |
| 80m |
| 4m/s?t |
| 60m |
t=
| 90 |
| 11 |
②如分析中图2,甲从B向C运动到M点,乙从C向A运动N点,△CMN∽△CBA,
所以
| CM |
| CB |
| CN |
| CA |
CM=60m-2m/s?t,CN=4m/s?t,
| 60m-2m/s?t |
| 60m |
| 4m/s?t |
| 80m |
所以,t=12s.
故答案为:6;
| 90 |
| 11 |
点评:本题重要的考查了相似三角形和二次函数的最小值,有点像数学题,尤其是相似三角形的两种情况,学生一般不容易考查全面,容易出现错误.

练习册系列答案
相关题目
 (2010?青浦区二模)在做“探究导体中电流与电压的关系”实验时,某小组同学利用A、B、C三个不同的导体作为研究对象分别接在如图所示的M、N两点间进行实验.表一、表二和表三为该小组同学的实验记录表.
(2010?青浦区二模)在做“探究导体中电流与电压的关系”实验时,某小组同学利用A、B、C三个不同的导体作为研究对象分别接在如图所示的M、N两点间进行实验.表一、表二和表三为该小组同学的实验记录表.
 如图所示,B、C两点相距60米,C、A两点相距80米,AC与BC相互垂直.甲以2米/秒的速度由B点向C点运动,乙以4米/秒的速度同时由C点向A点运动.经过________秒,甲、乙之间的距离最近;经过________秒,甲、乙所处位置与C点构成的三角形和三角形ABC可能相似.
如图所示,B、C两点相距60米,C、A两点相距80米,AC与BC相互垂直.甲以2米/秒的速度由B点向C点运动,乙以4米/秒的速度同时由C点向A点运动.经过________秒,甲、乙之间的距离最近;经过________秒,甲、乙所处位置与C点构成的三角形和三角形ABC可能相似.