题目内容

如图，杠杆AB是一根粗细均匀的木杆，其质量为116g；C是用细线拴在木杆0′点的铜铝合金球，其中含铝54g．现杠杆恰好在水平位置平衡．量得：AO'= $数学公式$ AB，A0= $数学公式$ AB．问：
（1）合金球C的总质量为多少？
（2）合金球C的平均密度为多少？（提示：先找出杠杆AB的重心O₁，再求出杠杆AB自身的重力G；列平衡方程，已知ρ_铝=2.7g/cm³ ρ_铜=8.9g/cm³）

解：（1）如图，D为杠杆的中点（重心）
∵AO′= $\text{[math]}$ AB，A0= $\text{[math]}$ AB，
∴OO′= $\text{[math]}$ OD，
∵杠杆在水平位置平衡，
∴G_C×OO′=G_杆×OD，即：m_Cg×OO′=m_杆×OD，
∴m_C= $\text{[math]}$ = $\text{[math]}$ =232g；
（2）合金球含铝m_铝=54g，铝的体积：
v_铝= 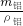$\text{[math]}$ = $\text{[math]}$ =20cm³，
合金球含铜m_铜=m_C-m_铝=232g-54g=178g，铜的体积：
v_铜= $\text{[math]}$ = $\text{[math]}$ =20cm³，
合金球的体积：
v=v_铜+v_铝=20cm³+20cm³=40cm³，
合金球的密度：
ρ_C= $\text{[math]}$ = $\text{[math]}$ =5.8g/cm³．
答：（1）合金球C的总质量为232g．
（2）合金球C的平均密度为5.8g/cm³．
分析：如图，求出OO′和OD的大小关系，知道杠杆的质量，利用杠杆的平衡条件求合金球的质量；
又知道合金球含铝的质量，可求含铜的质量，分别求出铝和铜的体积，利用总质量除以总体积可得合金球的密度．
点评：本题考查了学生对杠杆的平衡条件、密度公式的掌握和运用，计算合金球的密度要用总质量除以总体积，这是本题的关键．