题目内容
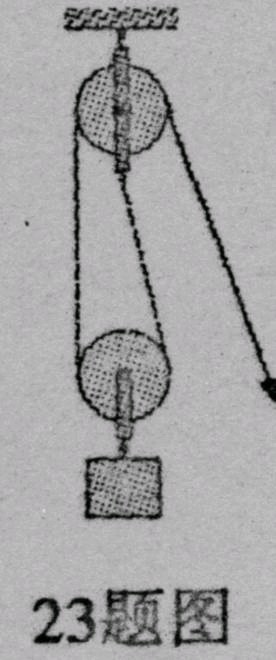
 工人利用如图所示的滑轮组将重400N的物体向上匀速提起2m.所用拉力为250N
工人利用如图所示的滑轮组将重400N的物体向上匀速提起2m.所用拉力为250N(1)滑轮组的机械效率是多少?
(2)若用此滑轮组将重900N的物体竖直向上匀速提升2m,拉力在这一过程中所做的功是多少?(不计绳重和摩擦力)
(解答要求:要写出依据的主要公式或变形公式,要有数据代入和运算结果)
分析:(1)由滑轮组装置可知承担物重的绳子股数n=2,重物被提升h,则拉力端移动的距离s=2h,知道物重G和升高的高度h求出有用功;知道拉力大小和拉力端移动的距离,求出总功W总=Fs,根据机械效率的公式求滑轮组的机械效率;
(2)求出了有用功、总功,由W总=W有用+W额计算出额外功,不计滑轮的摩擦和绳重,使用滑轮组做的额外功就是提升动滑轮做的功W额=G轮h,可以求出动滑轮重;
当提升重900N的物体时,不计滑轮的摩擦和绳重,F=
(G轮+G物),求出拉力F,再利用功的公式W=Fs求拉力在这一过程中所做的功.
(2)求出了有用功、总功,由W总=W有用+W额计算出额外功,不计滑轮的摩擦和绳重,使用滑轮组做的额外功就是提升动滑轮做的功W额=G轮h,可以求出动滑轮重;
当提升重900N的物体时,不计滑轮的摩擦和绳重,F=
| 1 |
| 2 |
解答:解:(1)由图可知,n=2,
∵h=2m,
∴s=2h=2×2m=4m;
当提升G=400N的重物时,
W有=Gh=400N×2m=800J;
W总=Fs=250N×4m=1000J,
滑轮组的机械效率:
η=
×100%=
×100%=80%.
(2)∵W总=W有用+W额,
∴W额=W总-W有用=1000J-800J=200J,
∵不计滑轮的摩擦和绳重,W额=G轮h,
∴G轮h=200J,即:G轮×2m=200J,
∴G轮=100N;
当提升重900N的物体时,
W有′=G′h=900N×2m=1800J;
不计滑轮的摩擦和绳重,
F′=
(G轮+G′)=
(100N+900N)=500N,
W总′=F′s=500N×4m=2000J,
答:(1)滑轮组的机械效率是80%;
(2)拉力在这一过程中所做的功为2000J.
∵h=2m,
∴s=2h=2×2m=4m;
当提升G=400N的重物时,
W有=Gh=400N×2m=800J;
W总=Fs=250N×4m=1000J,
滑轮组的机械效率:
η=
| W有 |
| W总 |
| 800J |
| 1000J |
(2)∵W总=W有用+W额,
∴W额=W总-W有用=1000J-800J=200J,
∵不计滑轮的摩擦和绳重,W额=G轮h,
∴G轮h=200J,即:G轮×2m=200J,
∴G轮=100N;
当提升重900N的物体时,
W有′=G′h=900N×2m=1800J;
不计滑轮的摩擦和绳重,
F′=
| 1 |
| 2 |
| 1 |
| 2 |
W总′=F′s=500N×4m=2000J,
答:(1)滑轮组的机械效率是80%;
(2)拉力在这一过程中所做的功为2000J.
点评:本题考查了使用滑轮组时有用功、总功、机械效率的计算方法,不计滑轮的摩擦和绳重,利用好“使用滑轮组做的额外功W额=G轮h,拉力F=
(G轮+G物)”是本题的关键.
| 1 |
| 2 |

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 工人利用如图所示的滑轮组提升重物,不计绳重和摩擦.
工人利用如图所示的滑轮组提升重物,不计绳重和摩擦. 工人利用如图所示的滑轮组提升重物,不计绳重和摩擦.
工人利用如图所示的滑轮组提升重物,不计绳重和摩擦.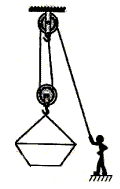


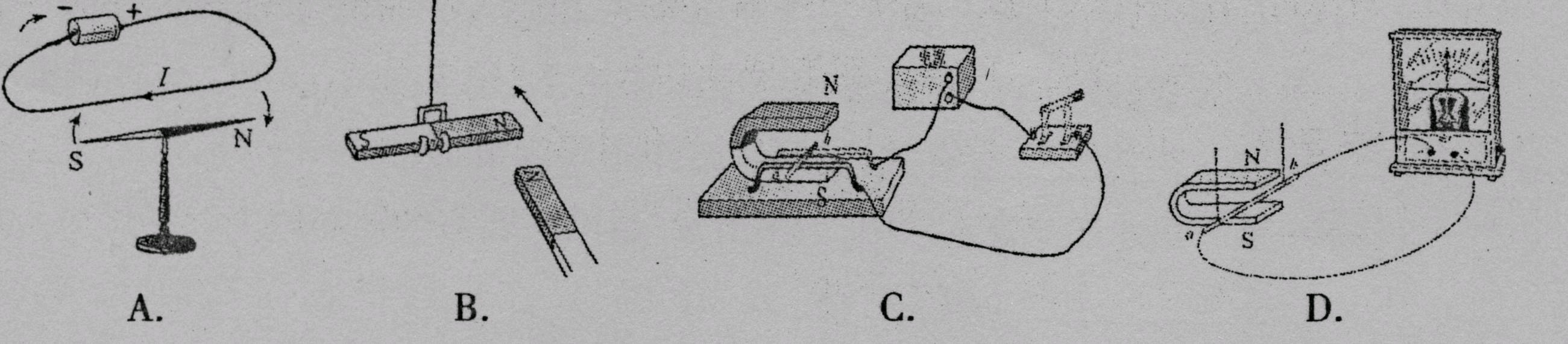
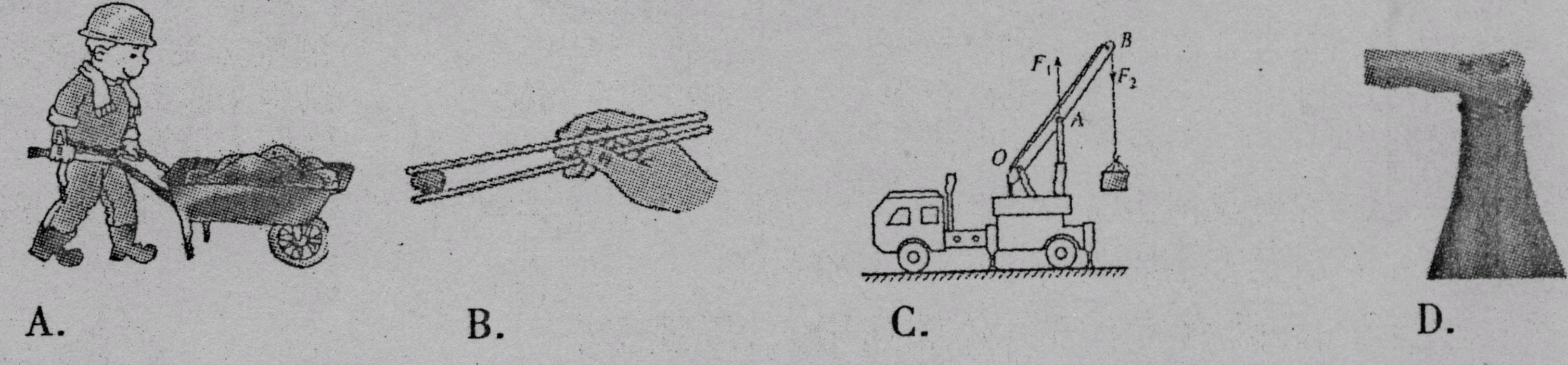
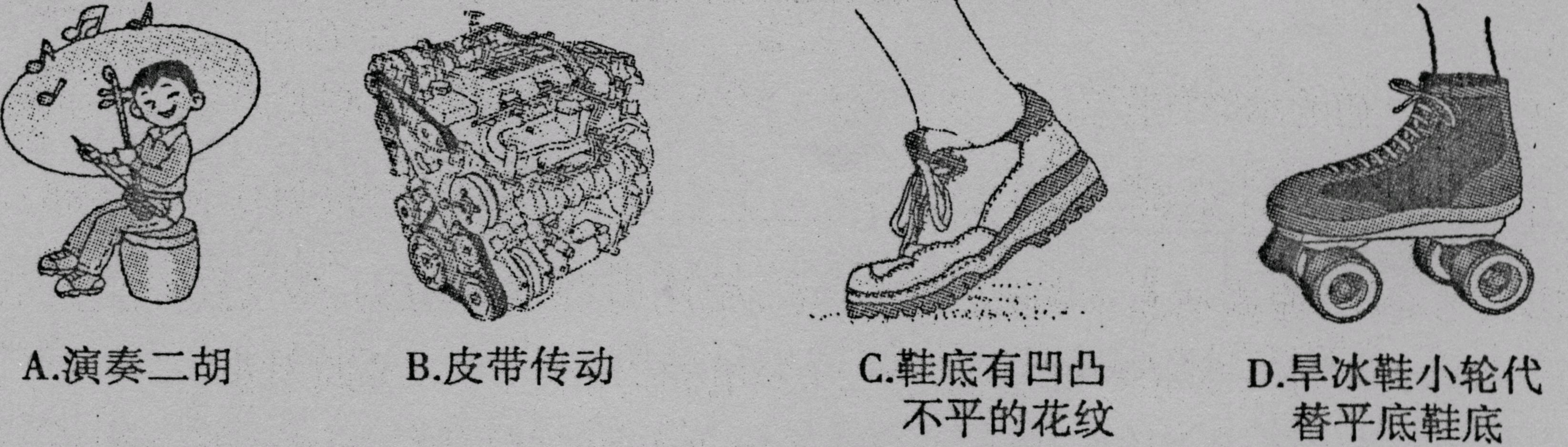 5.关于光学器材或设备,下列说法错误的是.( )
5.关于光学器材或设备,下列说法错误的是.( )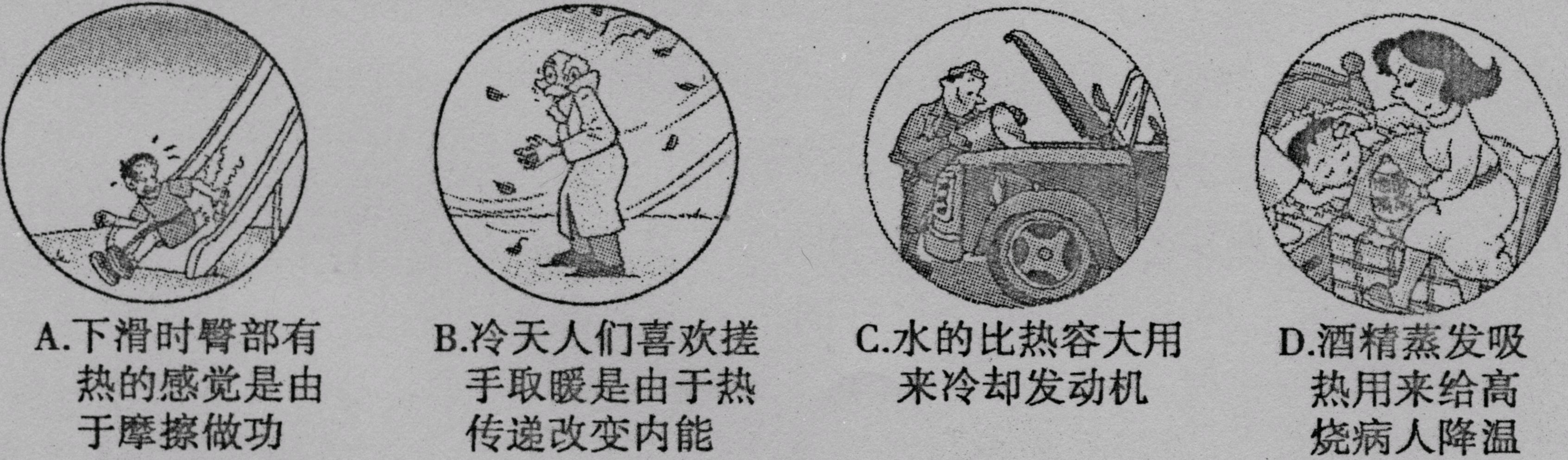


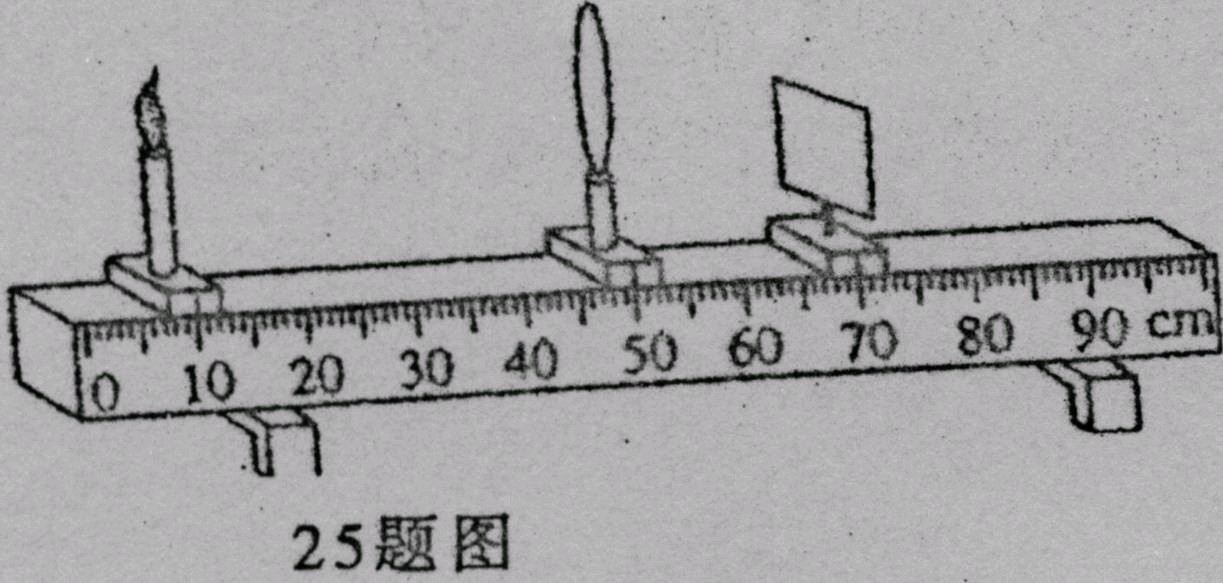
 25。如图所示,凸透镜的焦距为10cm,保持透镜位置不变,当蜡烛在10cm刻度处时,为了在光屏的中心找到像,应调整光屏的_______,并将光屏向_______方向移动(选填“远离透镜”或“靠近透镜").
25。如图所示,凸透镜的焦距为10cm,保持透镜位置不变,当蜡烛在10cm刻度处时,为了在光屏的中心找到像,应调整光屏的_______,并将光屏向_______方向移动(选填“远离透镜”或“靠近透镜").