题目内容
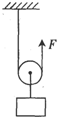
 如图所示,工人用滑轮组吊起质量为40kg的箱子,工人施加的拉力为250N,箱子被匀速竖直提升了2m,不计绳重和摩擦,取g=10N/kg,则滑轮组的机械效率为( )
如图所示,工人用滑轮组吊起质量为40kg的箱子,工人施加的拉力为250N,箱子被匀速竖直提升了2m,不计绳重和摩擦,取g=10N/kg,则滑轮组的机械效率为( )| A、62.5% | B、1 | C、80% | D、50% |
分析:由图可知,承担物重的绳子股数n=2,绳子末端移动的距离s=2h,有用功就是将箱子提升对箱子做的功(W有=Gh),拉力F做的功为总功(W总=Fs),再利用机械效率的公式求解;
解答:解:箱子被提升的高度h=2m,
拉力移动距离s=2h=2×2m=4m,
G=mg=40kg×10N/kg=400N,
W有=Gh=400N×2m=800J,
W总=Fs=250N×4m=1000J,
滑轮组的机械效率:
η=
×100%=
×100%=80%;
故选C.
拉力移动距离s=2h=2×2m=4m,
G=mg=40kg×10N/kg=400N,
W有=Gh=400N×2m=800J,
W总=Fs=250N×4m=1000J,
滑轮组的机械效率:
η=
| W有 |
| W总 |
| 800J |
| 1000J |
故选C.
点评:本题考查了有用功、总功、机械效率的计算方法,从滑轮组的结构找出n的值,求出绳子末端移动的距离s=nh是本题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图所示,工人用动滑轮将重400N的木箱匀速向上提升,不计摩擦和滑轮重,在此过程中,工人用的拉力为
如图所示,工人用动滑轮将重400N的木箱匀速向上提升,不计摩擦和滑轮重,在此过程中,工人用的拉力为 (2008?江宁区二模)如图所示,工人用一个动滑轮把重为800N的货物提到2m高处,所用的拉力是500N,则他做的有用功为
(2008?江宁区二模)如图所示,工人用一个动滑轮把重为800N的货物提到2m高处,所用的拉力是500N,则他做的有用功为 (2010?阿坝州)如图所示,工人用动滑轮将重400N的木箱匀速向上提升,不计摩擦、滑轮和绳重,在此过程中,工人用的拉力为
(2010?阿坝州)如图所示,工人用动滑轮将重400N的木箱匀速向上提升,不计摩擦、滑轮和绳重,在此过程中,工人用的拉力为 如图所示,工人用动滑轮将重200N的木箱匀速向上提升,不计摩擦和滑轮重,在此过程中,工人用的拉力为
如图所示,工人用动滑轮将重200N的木箱匀速向上提升,不计摩擦和滑轮重,在此过程中,工人用的拉力为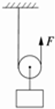 升国旗时,同学们会发现国旗杆上有一个滑轮,它是
升国旗时,同学们会发现国旗杆上有一个滑轮,它是