题目内容
 如图所示,在底面积为600cm2的圆柱形容器中,投入一体积为1×10-3m3的正方体木块,木块静止后,容器中水面上升的高度为2cm,则木块受到的浮力是________N,木块的密度是________kg/m3,投入木块后水对容器底部的压强与投入木块前水对容器底部的压强相比增大了________Pa.
如图所示,在底面积为600cm2的圆柱形容器中,投入一体积为1×10-3m3的正方体木块,木块静止后,容器中水面上升的高度为2cm,则木块受到的浮力是________N,木块的密度是________kg/m3,投入木块后水对容器底部的压强与投入木块前水对容器底部的压强相比增大了________Pa.
9.8 1000 196
分析:(1)知道正方体木块的体积可求木块的边长,进而求出木块排开水的体积,根据阿基米德原理求木块受到的浮力;
(2)对木块进行受力分析,由平衡条件求出木块的重力,然后求出木块的质量,最后由密度公式求出木块的密度.
(3)已知液面上升的高度,由液体压强公式求出容器增加的液体压强.
解答:(1)设木块的边长是a,则它的体积V=a3,
则木块的边长:a=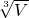 =
= =0.1m=10cm,
=0.1m=10cm,
木块排开水的体积:
V排=△S△h=(S容器-a2)△h=[600cm2-(10cm)2]×2cm=1000cm2=1×10-3m3,
木块受到的浮力:
F浮=ρ水gV排=1.0×103kg/m3×9.8N/kg×1×10-3m3=9.8N;
(2)木块受竖直向下的重力G,竖直向上的浮力F浮,
木块静止在水面上,处于平衡状态,
由平衡条件得:G=F浮=9.8N,
∵G=mg,
∴木块的质量m=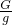 =
= =1kg,
=1kg,
木块的密度ρ木= =
= =1000kg/m3;
=1000kg/m3;
(3)投入木块后水对容器底部的压强与投入木块前水对容器底部的压强相比增大了
△p=ρg△h=1×103kg/m3×9.8N/kg×0.02m=196Pa;
故答案为:9.8;1000;196.
点评:本题考查了学生对阿基米德原理、液体压强公式、物体的漂浮条件的掌握和运用,本题难度不是很大,是一道中档题;灵活运用体积公式是本题的关键.
分析:(1)知道正方体木块的体积可求木块的边长,进而求出木块排开水的体积,根据阿基米德原理求木块受到的浮力;
(2)对木块进行受力分析,由平衡条件求出木块的重力,然后求出木块的质量,最后由密度公式求出木块的密度.
(3)已知液面上升的高度,由液体压强公式求出容器增加的液体压强.
解答:(1)设木块的边长是a,则它的体积V=a3,
则木块的边长:a=
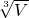 =
= =0.1m=10cm,
=0.1m=10cm,木块排开水的体积:
V排=△S△h=(S容器-a2)△h=[600cm2-(10cm)2]×2cm=1000cm2=1×10-3m3,
木块受到的浮力:
F浮=ρ水gV排=1.0×103kg/m3×9.8N/kg×1×10-3m3=9.8N;
(2)木块受竖直向下的重力G,竖直向上的浮力F浮,
木块静止在水面上,处于平衡状态,
由平衡条件得:G=F浮=9.8N,
∵G=mg,
∴木块的质量m=
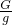 =
= =1kg,
=1kg,木块的密度ρ木=
 =
= =1000kg/m3;
=1000kg/m3;(3)投入木块后水对容器底部的压强与投入木块前水对容器底部的压强相比增大了
△p=ρg△h=1×103kg/m3×9.8N/kg×0.02m=196Pa;
故答案为:9.8;1000;196.
点评:本题考查了学生对阿基米德原理、液体压强公式、物体的漂浮条件的掌握和运用,本题难度不是很大,是一道中档题;灵活运用体积公式是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012?河西区一模)如图所示,在底面积为S1的圆柱形容器中注入水,把一横截面积为S2、高为h、密度为ρ柱的圆柱体直立于水中,圆柱体静止后,露出水面的高度为h1,此时水深为H.则下列说法中正确的是( )
(2012?河西区一模)如图所示,在底面积为S1的圆柱形容器中注入水,把一横截面积为S2、高为h、密度为ρ柱的圆柱体直立于水中,圆柱体静止后,露出水面的高度为h1,此时水深为H.则下列说法中正确的是( ) 如图所示,在底面积为S的圆柱形水池底部有一个金属球(球与池底没有密合),圆柱型的水槽漂浮在池内的水面上,此时水槽受到的浮力为F1.若把金属球从水中捞出并放在水槽中漂浮在水池中,此时水槽受到的浮力为F2,捞起金属球前、后水池底受到水的压强变化量为p,水的密度为ρ水.根据上述条件可以求出( )
如图所示,在底面积为S的圆柱形水池底部有一个金属球(球与池底没有密合),圆柱型的水槽漂浮在池内的水面上,此时水槽受到的浮力为F1.若把金属球从水中捞出并放在水槽中漂浮在水池中,此时水槽受到的浮力为F2,捞起金属球前、后水池底受到水的压强变化量为p,水的密度为ρ水.根据上述条件可以求出( ) (2008?海淀区一模)如图所示,在底面积为S的圆柱形水槽底部有一个金属球(球与槽底没有紧密接触),圆柱型的烧杯漂浮在水面上,此时烧杯受到的浮力为F1.若把金属球从水中捞出并放在烧杯里漂浮在水中,此时烧杯受到的浮力为F2,捞起金属球后水槽底部受到水的压强变化量为p,水的密度为ρ水.根据上述条件可知( )
(2008?海淀区一模)如图所示,在底面积为S的圆柱形水槽底部有一个金属球(球与槽底没有紧密接触),圆柱型的烧杯漂浮在水面上,此时烧杯受到的浮力为F1.若把金属球从水中捞出并放在烧杯里漂浮在水中,此时烧杯受到的浮力为F2,捞起金属球后水槽底部受到水的压强变化量为p,水的密度为ρ水.根据上述条件可知( ) (2009?朝阳区一模)如图所示,在底面积为S的圆柱形水槽底部有一个金属球,圆柱型的烧杯漂浮在水面上,此时烧杯底受到水的压力为F1.若把金属球从水中捞出放在烧杯里使其底部保持水平漂浮在水中,此时烧杯底受到水的压力为F2,此时水槽底部受到水的压强与捞起金属球前的变化量为p,水的密度为ρ水.根据上述条件可知金属球捞起放入烧杯后( )
(2009?朝阳区一模)如图所示,在底面积为S的圆柱形水槽底部有一个金属球,圆柱型的烧杯漂浮在水面上,此时烧杯底受到水的压力为F1.若把金属球从水中捞出放在烧杯里使其底部保持水平漂浮在水中,此时烧杯底受到水的压力为F2,此时水槽底部受到水的压强与捞起金属球前的变化量为p,水的密度为ρ水.根据上述条件可知金属球捞起放入烧杯后( ) 如图所示,在底面积为S的圆柱形水池底部有一个金属球(球与池底没有密合),圆柱型的水槽漂浮在池内的水面上,此时水槽受到的浮力为F1.若把金属球从水中捞出并放在水槽内漂浮在水池中,此时水槽受到的浮力为F2,捞起金属球前、后水池底受到水的压强变化量为p,水的密度为ρ水.则下列判断正确的是:( )
如图所示,在底面积为S的圆柱形水池底部有一个金属球(球与池底没有密合),圆柱型的水槽漂浮在池内的水面上,此时水槽受到的浮力为F1.若把金属球从水中捞出并放在水槽内漂浮在水池中,此时水槽受到的浮力为F2,捞起金属球前、后水池底受到水的压强变化量为p,水的密度为ρ水.则下列判断正确的是:( )