题目内容
一块边长为a的正方体合金块,是由密度分别为ρ1、ρ2的两种金属合成的.当将它放在水平桌面上时,对桌面的压强为p,求:
(1)合金块的质量;
(2)合金块的中ρ1金属所占的体积V1.
解:(1)合金块对地面的压力F=G=mg=ρVg,正方体合金块的体积V=a3,
∵P=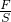 =
=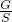 =
=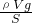 =ρgh,
=ρgh,
∴ρ= .
.
则合金块的质量m=ρV= ×a3=
×a3=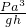 .
.
(2)密度为ρ2的金属质量m2=m-ρ1V1,体积V2= =
=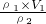 ,
,
ρ1金属所占的体积V1=V-V2=a3-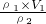 ,
,
化简得V1=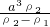 .
.
答:(1)合金块的质量为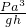 .
.
(2)合金块的中ρ1金属所占的体积V1=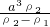 .
.
分析:(1)已知正方体的边长,可求其体积,因为是正方体合金块,对桌面的压强为P,所以可根据公式P=ρgh变形求得合金块的密度,再利用m=ρV可求合金块的质量;
(2)根据求得的合金的质量和已知ρ1、ρ2,可求得密度为ρ2的金属质量和体积,再用总体积减去密度为ρ2的金属的体积,化简即可.
点评:本题考查质量、重力、压力、压强等的计算,关键是公式及其变形的灵活运用;突破点是混合后体积不变,还要知道物体对地面的压力等于物体自身的重力.
∵P=
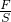 =
=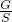 =
=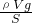 =ρgh,
=ρgh,∴ρ=
 .
.则合金块的质量m=ρV=
 ×a3=
×a3=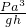 .
.(2)密度为ρ2的金属质量m2=m-ρ1V1,体积V2=
 =
=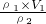 ,
,ρ1金属所占的体积V1=V-V2=a3-
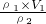 ,
,化简得V1=
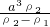 .
.答:(1)合金块的质量为
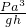 .
.(2)合金块的中ρ1金属所占的体积V1=
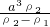 .
.分析:(1)已知正方体的边长,可求其体积,因为是正方体合金块,对桌面的压强为P,所以可根据公式P=ρgh变形求得合金块的密度,再利用m=ρV可求合金块的质量;
(2)根据求得的合金的质量和已知ρ1、ρ2,可求得密度为ρ2的金属质量和体积,再用总体积减去密度为ρ2的金属的体积,化简即可.
点评:本题考查质量、重力、压力、压强等的计算,关键是公式及其变形的灵活运用;突破点是混合后体积不变,还要知道物体对地面的压力等于物体自身的重力.

练习册系列答案
相关题目
